Bipart
Application Description
This benchmark produces a k-way partitioning of a hypergraph. It implements a multi-level partitioning algorithm proposed by Smaleki et al.. The data parallelism in this algorithm arises from hyperedges in the hypergraph that can be processed in parallel.
Algorithm
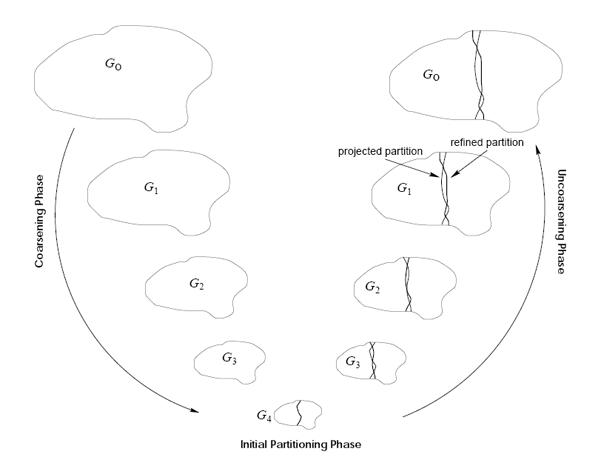
BiPart is a multi-level partitioning algorithm. It first iteratively coarsens the hypergraph by collapsing nodes until the graph is small enough, then it uses a greedy algorithm to produce a bi-partitioning of the small hypergraph, and finally it projects the partitioning back to the original hypergraph. During each projection to the next finer graph, it refines the partitioning. Figure 1 shows a multi-level graph partitioning. Below, we explain each level briefly.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | Input: coarseGraph, fineGraph, policy for all hyperedge hedge in fineGraph in parallel do Let S be the set of nodes that are matched to hedge in M. Merge nodes in S together to form a single node N in coarseGraph. for all node in S do N <- parent(node) for all hyperedge hedge in fineGraph in parallel do Let S be the set of nodes that are matched to hedge in M. if |S| = 1 and there exist an already merged node v 2 hedge then Let v be the merged node in hedge with smallest weight. Merge node in S with v; parent(S) <- parent(v) for all hyperedge hedge 2 fineGraph in parallel do parents = NULL for all node 2 hedge do if parent(node) not in parents then parents.add(parent(node)) Hedge <- coarseGraph.createHyperedge() Hedge <- parent(hedge) for all node 2 parents do createEdge(Hedge, node) |
Figure 2: Pseudocode for the coarsening phase.
| 1 2 3 4 5 6 7 8 9 | Given coarsest graph G = (V,E). P and Pc are sets of nodes. P = {}. Pc = V. n = |V|. Compute move gain values for each node in Pc. repeat Pick top sqrt(n) nodes from Pc with highest gain values (break ties using node ID). Let M denote the set of these nodes. Move nodes in M to P in parallel. Re-compute move gain values for nodes in Pc. until balance is achieved |
Figure 3: Pseudocode for the initial partitioning
| 1 2 3 4 5 6 7 8 9 | input: iter: refinement iterations Initialization: Project bipartition from coarsened graph. for iter iterations do Compute move gain values for all nodes. l0 <- nodes in partition 0 with gain value >= 0. l1 <- nodes in partition 1 with gain value >= 0. Sort nodes in l0 and l1 with gain value as the key (break ties using node IDs). lmin <- min (|l0|, |l1|). Swap lmin nodes with highest gain values between partitions l0 and l1 in parallel. Check if the balance criterion is satisfied. Otherwise move highest gain value nodes from the higher weighted partition to the other partition. |
Figure 4: Pseudocode for the refinement phase.
| 1 2 3 4 5 6 7 8 9 10 11 | Input: Graph G = (V,E). for each hyperedge hedge 2 E in parallel do p0 = number of nodes in partition 0 p1 = number of nodes in partition 1 for u in hedge do i <- partition of u if pi == 1 then FS(u) <- FS(u) + 1 else if pi == |hedge| then TE(u) <- TE(u) + 1 for u in V in parallel do Gain(u) <- FS(u) − TE(u) |
Figure 5: Pseudocode for computing move-gain values.
Performance
Figure 6 shows the relative speedup of deterministic Galois-BiPart compared to Zoltan [1] with 14 threads. Figure 7 shows strong scaling performance of BiPart.
[1] K. D. Devine, E. G. Boman, R. T. Heaphy, R. H. Bisseling and U. V. Catalyurek, "Parallel hypergraph partitioning for scientific computing," Proceedings 20th IEEE International Parallel and Distributed Processing Symposium, Rhodes Island, 2006.
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
