Parallel Graphs

For graph computation, Galois provides unified, standard APIs to access graph elements as well as a set of graph implementations optimized for NUMA-awareness, conflict detection and interoperability with the Galois runtime system. All graphs are in the namespace galois::graphs.

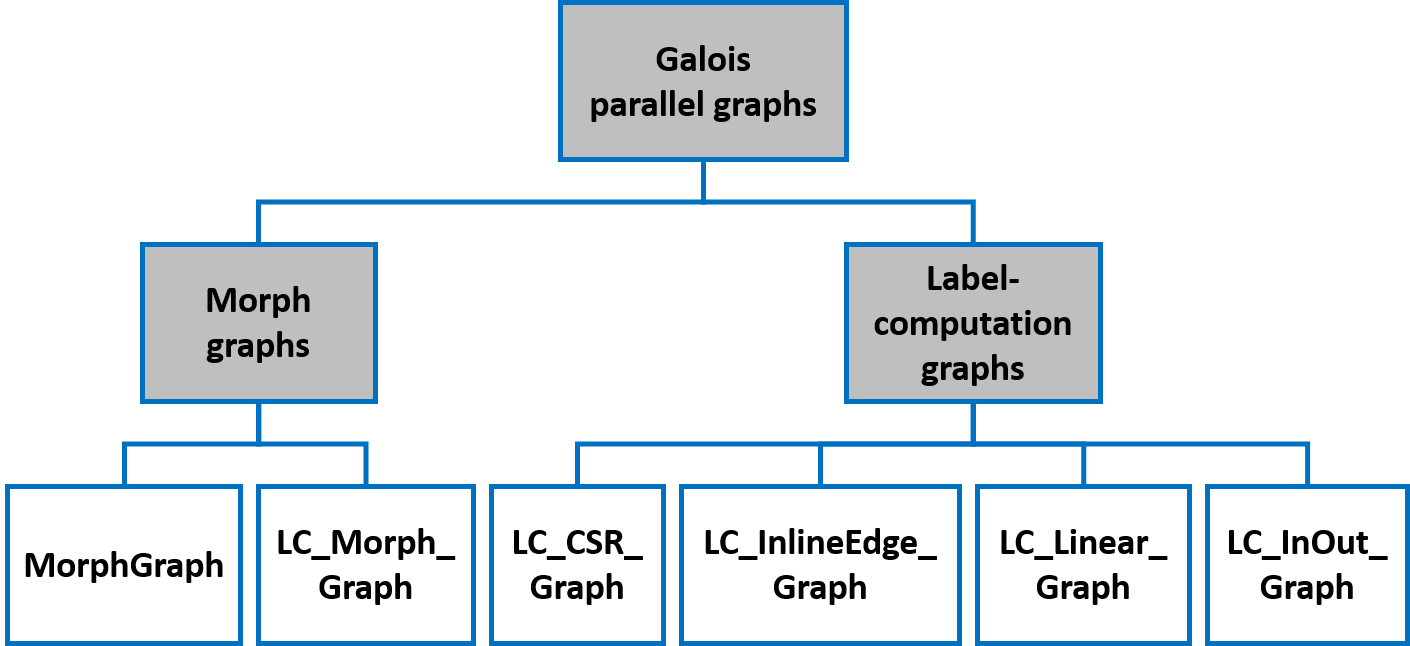
Galois Parallel Graphs

There are two types of graphs, summarized pictorially as the above hierarchy.

galois::graphs::MorphGraph: This graph type allows insertion and removal of nodes and edges. It is used in morph algorithms like Delaunay mesh refinement. A variation called galois::graphs::LC_Morph_Graph can be used if (1) node removals are impossible, and (2) when a node is created, its maximum degree is known.
galois::graphs::LC_CSR_Graph: This graph type disallows creation and removal of nodes and edges. Internally, it is implemented with compressed sparse row format, as shown in the following figure. Undirected edges must be represented as two directed edges. Galois also provides variants of this graph with different layouts in memory, e.g. galois::graphs::LC_InlineEdge_Graph, galois::graphs::LC_Linear_Graph, galois::graphs::LC_InOut_Graph.

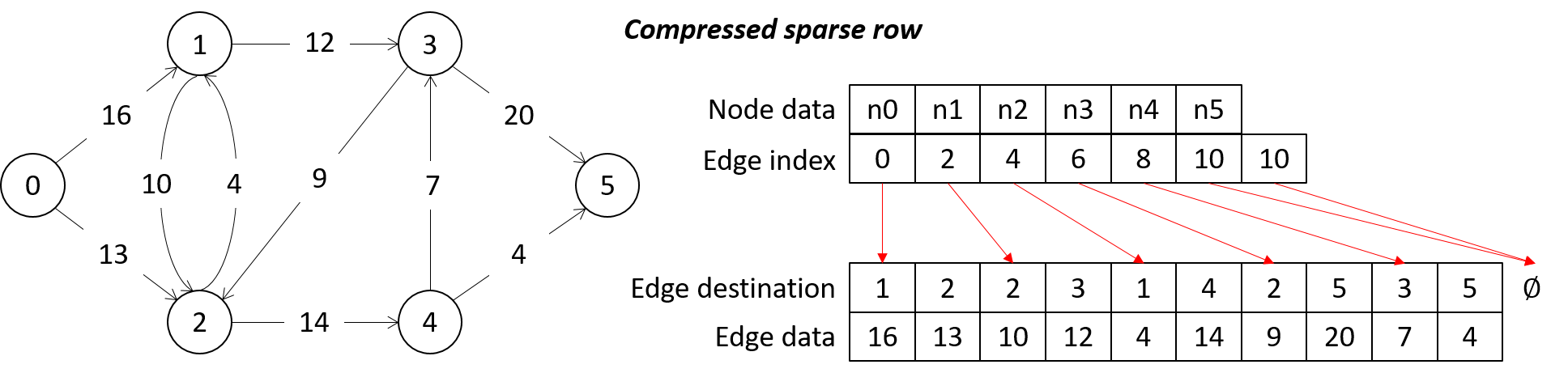
Graph in CSR Format

Label-computation Graphs

Template Parameters

When defining a galois::graphs::LC_CSR_Graph, the following template parameters are required:

NodeTy: the type of data stored on each node. Use void when no data needs to be stored on nodes.
EdgeTy: the type of data stored on each edge. Use void when no data needs to be stored on edges.

The following features can be enabled using the corresponding graph member type definitions:

Use galois::graphs::LC_CSR_Graph::with_no_lockable< true >::type to remove abstract node locks and conflict detections.
Use galois::graphs::LC_CSR_Graph::with_numa_alloc< true >::type to enable NUMA-aware allocation.
Use galois::graphs::LC_CSR_Graph::with_out_of_line_lockable< true >::type to separate node locks from nodes.

See galois::graphs::LC_CSR_Graph for more details on which template parameters are available and what they mean.

These member type definitions can be chained together to get a graph type with multiple options specified. Below is an example of defining an LC_CSR_Graph with node data of type std::atomic<uint32_t>, edge data of type uint32_t, node locks removed and NUMA-aware allocation enabled:

using Graph = galois::graphs::LC_CSR_Graph<std::atomic<uint32_t>, uint32_t>::

with_no_lockable<true>::type ::with_numa_alloc<true>::type;

APIs

The following code snippet shows how to instantiate and read in a graph from a file (in binary gr format):

Graph g;

galois::graphs::readGraph(g, argv[1]); // argv[1] is the file name for graph

To access graph elements, use the following constructs.

Iteration over nodes: use the node iterator galois::graphs::LC_CSR_Graph::iterator given by galois::graphs::LC_CSR_Graph::begin and galois::graphs::LC_CSR_Graph::end.
Iteration over outgoing edges of a node: use the edge iterator galois::graphs::LC_CSR_Graph::edge_iterator given by galois::graphs::LC_CSR_Graph::edge_begin and galois::graphs::LC_CSR_Graph::edge_end. By default, the outgoing neighbors of the node are locked by these operations.
To read/write a node's data: use galois::graphs::LC_CSR_Graph::getData. By default, the node is locked by this operation.
To read/write an edge's data: use galois::graphs::LC_CSR_Graph::getEdgeData.
To access the destination node of an outgoing edge: use galois::graphs::LC_CSR_Graph::getEdgeDst.
To query the number of nodes: use galois::graphs::LC_CSR_Graph::size.
To query the number of outgoing edges: use galois::graphs::LC_CSR_Graph::sizeEdges.

See galois::graphs::LC_CSR_Graph for other available APIs, e.g. those for sorting edges for a node and searching for a specific edge.

The following example from lonestar/tutorial_examples/GraphTraversalSerial.cpp iterates through all nodes, and for each node, adds all outgoing edges' weights to the node data. This example is written in C++11 to avoid mentioning node iterators and edge iterators explicitly.

  // iterate over nodes
  for (auto n : g) {
    auto& sum = g.getData(n); // get node data of n
    sum       = 0;
    // iterate over edges from node n
    for (auto e : g.edges(n)) {
      sum += g.getEdgeData(e); // get edge data of e
    }
  }

To avoid locking nodes and conflict detection, pass galois::MethodFlag::UNPROTECTED to getData(), edge_begin(), edge_end() or edges() as the following example from lonestar/tutorial_examples/ConflictAwareTorus.cpp:

  // serial verification, no conflict is possible
  size_t numWrongAnswer = 0;
  for (auto n : torus) {
    // use galois::MethodFlag::UNPROTECTED to notify Galois runtime
    // that do not acquire lock for this call
    if (torus.getData(n, galois::MethodFlag::UNPROTECTED) != 4) {
      numWrongAnswer++;
    }
  }
  std::cout << "# nodes of wrong answer: " << numWrongAnswer << std::endl;

Different Storage Formats

Galois provides two variants for galois::graphs::LC_CSR_Graph: galois::graphs::LC_InlineEdge_Graph and galois::graphs::LC_Linear_Graph. They all support the same functionalities but with different storage formats, as shown in the following figure. The differences come from merging arrays in CSR format to enhance spatial locality for certain access patterns.

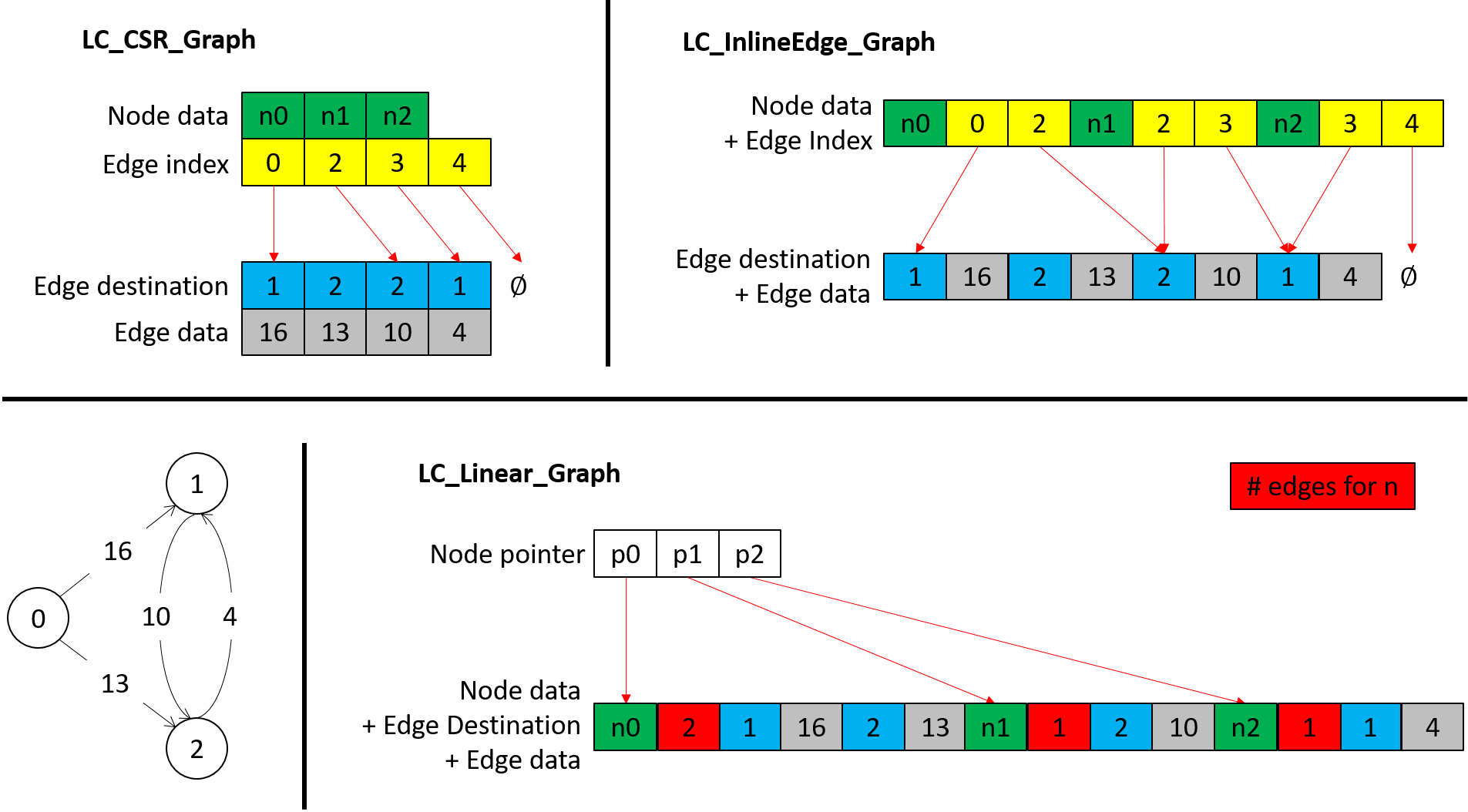
Differences of Galois label-computation graphs

galois::graphs::LC_Adaptor_Graph helps with creating types with custom data layouts that provide the same APIs as galois::graphs::LC_CSR_Graph

Tracking Incoming Edges

galois::graphs::LC_InOut_Graph can be used if the desired computation needs to track incoming edges. Below is an example of defining a galois::graphs::LC_InOut_Graph:

using InnerGraph = galois::graphs::LC_CSR_Graph<int, void>::with_no_lockable< true >::type;
using Graph = galois::graphs::LC_InOut_Graph<InnerGraph>;
using GNode = Graph::GraphNode;

If the graph is not symmetric, then both the original and the transposed binary graphs are required to initialize a galois::graphs::LC_InOut_Graph, as the following code snippet shows.

Graph g;

galois::graphs::readGraph(g, original_graph_name, transposed_graph_name);

The functionality of a galois::graphs::LC_InOut_Graph is the same as the inner LC_Graph, e.g. galois::graphs::LC_CSR_Graph. Additionally, it is possible to iterate over incoming edges/neighbors with the following methods.

To iterate over the incoming edges of a node, use galois::graphs::LC_InOut_Graph::in_edge_iterator given by galois::graphs::LC_InOut_Graph::in_edge_begin and galois::graphs::LC_InOut_Graph::in_edge_end.
To get access to the destination of an incoming edge, use galois::graphs::LC_InOut_Graph::getInEdgeDst.
To read/write an incoming edge's data, use galois::graphs::LC_InOut_Graph::getInEdgeData.

The data for incoming edges are stored by value. Users are responsible for maintaining the consistency of outgoing edges and corresponding incoming edges.

Morph Graphs

galois::graphs::MorphGraph can be used in cases where an application requires modifying graph topology.

Template Parameters

galois::graphs::MorphGraph takes the following template parameters:

NodeTy: the type of data stored on nodes. Use void if there is no data stored on nodes.
EdgeTy: the type of data stored on edges. Use void if there is no data stored on edges.
Directional: a boolean variable indicating whether this is a directed graph. If not, then each edges will have its symmetric counterpart, all represented as outgoing edges.
InOut: a boolean variable indicating whether incoming edges are tracked. If Directional and InOut are both true, then each edge will have its incoming counterpart. This is default to false.

Note that an edge and its symmetric/incoming counterpart share edge data.

The following features can be enabled using the corresponding graph member type definitions.

Use galois::graphs::MorphGraph::with_no_lockable< true >::type to remove node locks and turn off conflict detection.
Use galois::graphs::MorphGraph::with_sorted_neighbors< true >::type to have the edge lists of nodes always sorted.

Below is an example of defining a directed galois::graphs::MorphGraph with integer node data, no edge data, and no tracking incoming edges. Neighbors of each node are always sorted.

// Graph has int node data, void edge data and is directed w/o tracking incoming edges. Neighbors of each node are always sorted.
using Graph = galois::graphs::MorphGraph<int,void,true,false>::with_sorted_neighbors<true>::type;
// typedef for graph nodes
using GNode = Graph::GraphNode;

APIs

galois::graphs::MorphGraph supports all the functionalities in galois::graphs::LC_CSR_Graph except for size() and sizeEdges(). Additionally, galois::graphs::MorphGraph provides the following APIs to modify graph topology:

galois::graphs::MorphGraph::createNode allocates space for node data, and galois::graphs::MorphGraph::addNode adds to a graph a node already allocated by galois::graphs::MorphGraph::createNode.
galois::graphs::MorphGraph::addEdge and galois::graphs::MorphGraph::addMultiEdge both add an edge between existing nodes in a graph. The former adds an edge only when the edge does not exist, while the latter always adds the edge. The incoming/symmetric counterpart of the edge will also be added if tracked. Lock for an edge's source node is always acquired, and that for the destination node is also acquired if incoming/symmetric edges are tracked.
galois::graphs::MorphGraph::removeNode removes a node from a graph along with any incoming or outgoing edges associated with that node. Only the node being removed is locked.
galois::graphs::MorphGraph::removeEdge removes an edge from a graph along with its incoming/symmetric counterpart, if there is one. Nodes are locked in the same way as in galois::graphs::MorphGraph::addEdge.

See galois::graphs::MorphGraph for other available APIs for things like sorting the edges of a node and searching for a specific edge.

The following code snippet shows how to add nodes and edges to a galois::graphs::MorphGraph. Note that the nodes must be created first, then added to a galois::graphs::MorphGraph. Once that is done, edges can be added between the nodes.

void constructTorus(Graph& g, int height, int width) {
  // Construct set of nodes
  int numNodes = height * width;
  std::vector<GNode> nodes(numNodes);
  for (int i = 0; i < numNodes; ++i) {
    GNode n = g.createNode(
        0);       // allocate node data and initialize the node data with 0
    g.addNode(n); // add n to g. from now on n can be located from g
    nodes[i] = n;
  }
  // Add edges
  for (int x = 0; x < width; ++x) {
    for (int y = 0; y < height; ++y) {
      GNode c = nodes[x * height + y];
      GNode n = nodes[x * height + ((y + 1) % height)];
      GNode s = nodes[x * height + ((y - 1 + height) % height)];
      GNode e = nodes[((x + 1) % width) * height + y];
      GNode w = nodes[((x - 1 + width) % width) * height + y];
      g.addEdge(c, n); // addEdge checks if the edge exists or not. nop if so.
      g.addEdge(c, s);
      g.addEdge(c, e);
      g.addEdge(c, w);
    }
  }
}

See the full example at lonestar/tutorial_examples/TorusConstruction.cpp

LC_Morph_Graph

If node removals are not allowed and the maximum degree of a node is known when creating the node, then galois::graphs::LC_Morph_Graph can be used.

The template parameters and features of galois::graphs::LC_Morph_Graph are the same as those of galois::graphs::LC_CSR_Graph.

The APIs of galois::graphs::LC_Morph_Graph are the same with those of galois::graphs::MorphGraph with the following exceptions.

galois::graphs::LC_Morph_Graph has no method of removeNode.
galois::graphs::LC_Morph_Graph::createNode will allocate node data and add the node to the graph.
If a galois::graphs::LC_Morph_Graph is meant to be symmetric, then the user is responsible for maintaining the symmetry. In particular, this matters when using the following functions:

Since symmetry is maintained by the user, only the lock for the source node of an edge is acquired when calling galois::graphs::LC_Morph_Graph::addEdge, galois::graphs::LC_Morph_Graph::addMultiEdge, and galois::graphs::LC_Morph_Graph::removeEdge.

Insert Bag

galois::InsertBag is an unordered collection that allows parallel insertions. It uses customized memory allocations to achieve scalable parallel insertions.

galois::InsertBag expects a template parameter, T, for the type of elements that the galois::InsertBag contains. See galois::InsertBag for other optional template parameters.

An example of defining a galois::InsertBag follows:

// BasePoints expands to galois::InsertBag<Point>

BasePoints basePoints;

galois::InsertBag::emplace is used to insert elements, which are constructed in-place in the bag using an appropriate constructor for the element. galois::InsertBag::push and galois::InsertBag::push_back are shortcuts of galois::InsertBag::emplace. An example of inserting elements into a galois::InsertBag follows:

    // basePoints is of type galois::InsertBag<Point>
    // points is of type std::vector<Point>
    Point* p1 = &(basePoints.push(points[last - 1]));
    Point* p2 = &(basePoints.push(points[last - 2]));
    Point* p3 = &(basePoints.push(points[last - 3]));

Accessing the elements is only allowed in serial. galois::InsertBag::begin and galois::InsertBag::end are used to access the elements. galois::InsertBag::empty is used to check if the bag is empty. An example of accessing elements inside a galois::InsertBag follows. Note that this example is written in C++11 to avoid mentioning galois::InsertBag::begin and galois::InsertBag::end explicitly.

    // PtrPoints expands to galois::InsertBag<Point*>
    // points is of type std::vector<Point>
    PtrPoints& pptrs = *rounds[i];
    for (auto ii : pptrs) {
      points.push_back(*ii);
    }

Table of Contents

Parallel Graphs

Label-computation Graphs

Template Parameters

APIs

Different Storage Formats

Tracking Incoming Edges

Morph Graphs

Template Parameters

APIs

LC_Morph_Graph

Insert Bag