Reduction Operations

Table of Contents

• Introduction
• Scalar Reduction
  • Defining a Reducer
  • Reducing Values
  • Example

Introduction

Reduction is a fundamental operation used in different graph analytics problems such as bread-first search (BFS), connected components (CC), and PageRank (PR). As such, the Galois runtime provides support for different types of reduction operations such as addition (also known as accumulation).

Data structures that support reductions in Galois are conceptually divided into two classes: reduction of scalar types (e.g., ints and floats) or reduction of container types (e.g., STL vectors and maps).

Scalar Reduction

galois::Reducible is the base class to help reduce values of primitive types or types that are cheap to copy. For example, galois::GAccumulator is for accumulating values of types such as ints.

Defining a Reducer

galois::Reducible is used to reduce mutliple values of type T to a single value. It is optimized for basic types or types that have low overheads while copying. galois::Reducible takes the type T of the values to be reduced and a functor MergeFunc as template parameters, where the MergeFunc conforms to:

T operator()(const T& a, const T& b);

Reducing Values

galois::Reducible starts with the default value of type T. galois::Reducible::update() updates the thread local value by applying the reduction operator to the thread local and provided value. After a parallel region, the final value can be retrieved using galois::Reducible::reduce(). Note, that galois::Reducible::reduce() can only be used outside of parallel regions (e.g., galois::for_each).

The following figure shows the inheritance hierarachy of Galois classes that implement support for scalar reduction operations.

Scalar reducers in Galois

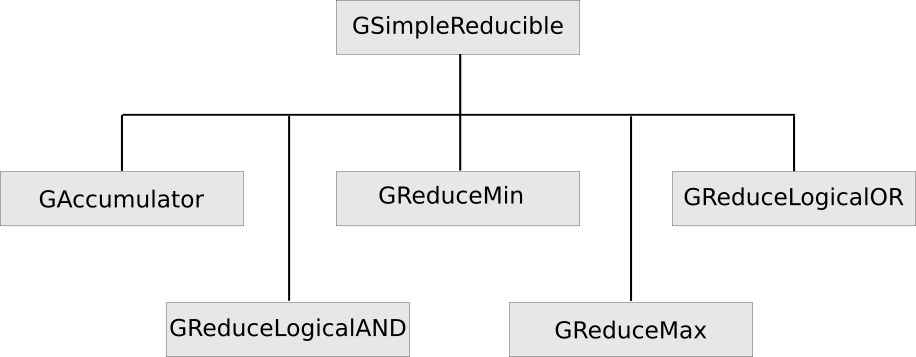
These specialized reducer classes implement support for different types of reduction operations by inheriting from galois::Reducible:

• galois::GAccumulator is used to accumulate a set of values. It provides galois::GAccumulator::operator+= and galois::GAccumulator::operator-= for adding or subtracting values.
• galois::GReduceMax is used to reduce to the maximum value. Type T has to meet the type requirements of std::max.
• galois::GReduceMin is used to reduce to the minimum value. Type T has to meet the type requirements of std::min.
• galois::GReduceLogicalAnd is used to perform a logical and of the accumulated values. Type T has to meet the type requirements of std::logical_and.
• galois::GReduceLogicalOr is used to perform a logical or of the accumulated values. Type T has to meet the type requirements of std::logical_or.

Example

In the following, we show an example of using reduction operations in a common graph analytics application, PageRank. The residual pull-based algorithm for PageRank uses galois::GAccumulator to keep track of whether a node with outgoing neighbors has new PageRank contribution that needs to be propagated. The PageRank computation can terminate if the reduced value across all nodes in the graph is zero (i.e., implying no more work).

void computePRResidual(Graph& graph, DeltaArray& delta,
                       ResidualArray& residual) {
  unsigned int iterations = 0;
  galois::GAccumulator<unsigned int> accum;

  while (true) {
    galois::do_all(
        galois::iterate(graph),
        [&](const GNode& src) {
          auto& sdata = graph.getData(src);
          delta[src]  = 0;

          if (residual[src] > tolerance) {
            PRTy oldResidual = residual[src];
            residual[src]    = 0.0;
            sdata.value += oldResidual;
            if (sdata.nout > 0) {
              delta[src] = oldResidual * ALPHA / sdata.nout;
              accum += 1;
            }
          }
        },
        galois::no_stats(), galois::loopname("PageRank_delta"));

    galois::do_all(
        galois::iterate(graph),
        [&](const GNode& src) {
          float sum = 0;
          for (auto nbr : graph.edges(src)) {
            GNode dst = graph.getEdgeDst(nbr);
            if (delta[dst] > 0) {
              sum += delta[dst];
            }
          }
          if (sum > 0) {
            residual[src] = sum;
          }
        },
        galois::steal(), galois::chunk_size<CHUNK_SIZE>(), galois::no_stats(),
        galois::loopname("PageRank"));

#if DEBUG
    std::cout << "iteration: " << iterations << "\n";
#endif
    iterations++;
    if (iterations >= maxIterations || !accum.reduce()) {
      break;
    }
    accum.reset();
  }