|
Galois
|
|
Galois
|
This tutorial is targeted to people who want to start writing Galois programs, which are legal C++ parallel programs. It assumes that readers are familiar with C++ and have some knowledge about parallel programming.
The following topics are outside the scope of this tutorial:
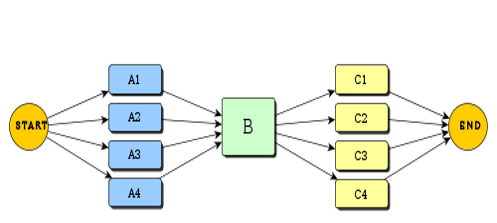
A Galois program alternates its execution in between serial and parallel phases. The execution begins serially on the master thread, whose thread ID is 0. Other threads wait in a "sleep" state in galois::substrate::ThreadPool, which is created by galois::SharedMemSys. Upon encountering a parallel section, the Galois runtime wakes up the threads in cascade, and hands each thread a work function. Threads synchronize at a barrier at the end of the parallel section. In the current implementation, parallel sections are loops and work items are iterations of that loop. This is summarized in the following figure.
Galois is different from other models in the following two ways.
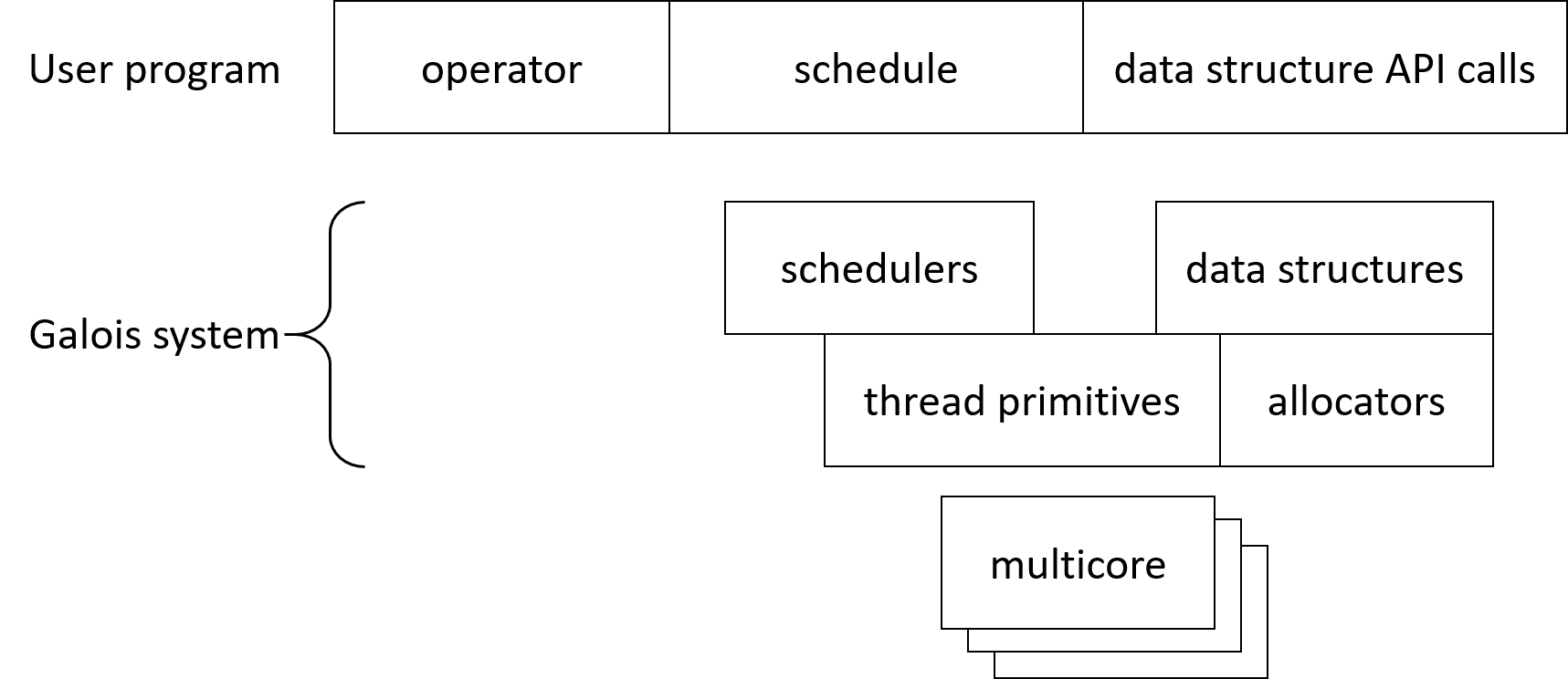
A Galois user program consists of operators, schedules and data structure API calls. The Galois library implements schedulers and data structures, which are built upon thread primitives and memory allocators. This is summarized by the following figure.
galois::SharedMemSys must be declared and constructed before any other Galois features can be used, since it creates galois::substrate::ThreadPool and other runtime structures, on which several Galois features depend.
Throughout this tutorial, we will use the following application as our running example: read in an undirected graph with edge weights, and then set the label of each node to the sum of the weights on the edges connected to the node. There are two ways to implement this application. If it is implemented as a pull-style algorithm, each node iterates over its edges and computes its own label; there are no conflicts among activities at different nodes. However, when it is implemented as a push-style algorithm, each node iterates over its edges and for each edge, the node updates the weight of the destination node. Therefore, activities may conflict with each other. Both variants iterate over all nodes, so they are topology-driven algorithms.
Below we will cover parallel data structures, parallel loop iterators, and worklists and schedules.
For graph computation, Galois provides unified, standard APIs to access graph elements and a set of graph implementations optimized for NUMA-awareness, conflict detection and interoperability with the Galois runtime system. All graphs are in the namespace galois::graphs. There are two types of graphs:
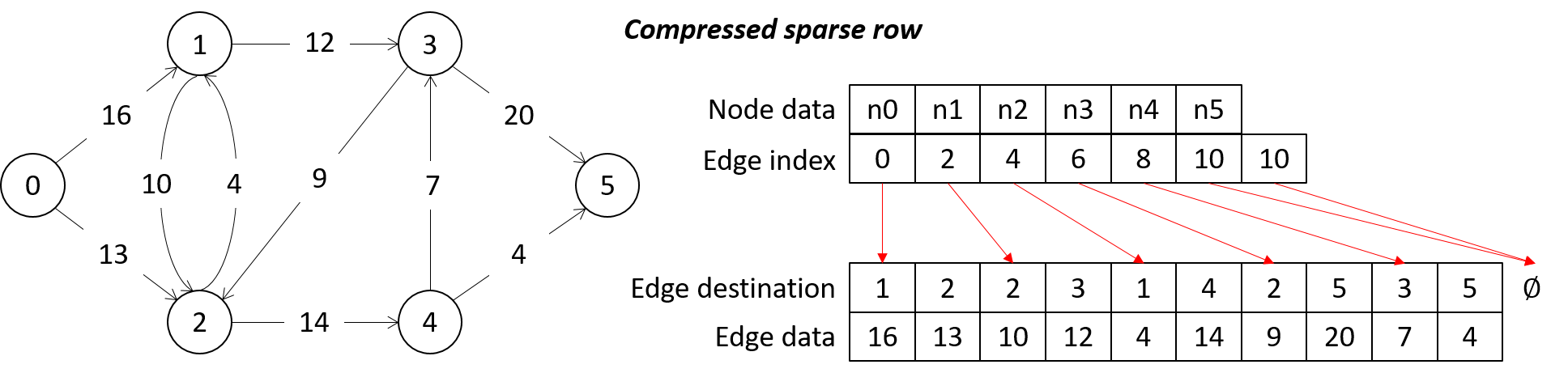
Other data structures available in Galois are galois::InsertBag, an unordered bag allowing thread-safe concurrent insertion; galois::GSimpleReducible, a template for scalar reduction; and galois::GBigReducible, a template for container reduction. We will focus on galois::graphs::LC_CSR_Graph in this section.
When defining a galois::graphs::LC_CSR_Graph, you must provide as template parameters NodeTy, the type of data stored on each node; and EdgeTy, the type of data stored on each edge. Use void when no data needs to be stored on nodes or edges. See galois::graphs::LC_CSR_Graph for other optional template parameters.
Below is an example of defining an LC_CSR_Graph with an integer as both its node data type and edge data type:
The following code snippet shows how to instantiate and read in a graph from a file (in binary gr format):
To access graph elements, use the following constructs.
The following example is a serial implementation of our running example. It is a pull-style implementation: iterate through all nodes, and for each node, add all outgoing edges' weights to the node data. This example is written in C++11 to avoid mentioning node iterators and edge iterators explicitly.
The full example is available as lonestar/tutorial_examples/GraphTraversalSerial.cpp
galois::do_all partitions the work items evenly among threads, and each thread performs work independently. It turns off conflict detection and assumes no new work items are created. Work stealing can be turned on to achieve load balance among threads. Example usages of galois::do_all are topology-driven algorithms iterating over nodes in a graph; and bags with independent work items, e.g. subset of nodes in a graph.
Specifically, galois::do_all expects the following inputs:
Below is the example of parallelizing our running example with a pull-style operator using galois::do_all. Note that the range for this do_all call is exactly the outer loop range in the serial implementation, and that the operator is exactly the body of the outer loop in our serial implementation.
The full example is available as lonestar/tutorial_examples/GraphTraversalPullOperator.cpp
How work is divided among threads in galois::do_all depends on whether work stealing is turned on. If work stealing is turned off, then the range is partitioned evenly among threads, and each thread works on its own partition independently. If work stealing is turned on, the work range is partitioned into chunks of N iterations, where N is the chunk size. Each thread is then assigned an initial set of chunks and starts working from the beginning of the set. If a thread finishes its own chunks but other threads are still working on theirs, it will steal chunks from another thread's end of set of chunks.
galois::for_each can be used for parallel iterations that may generate new work items, and that may have conflicts among iterations. Operators must be cautious: All locks should be acquired successfully before the first write to user state. Optional features for galois::for_each include (1) turning off conflict detection, (2) asserting that no new work items will be created, and (3) specifying a desired schedule for processing active elements. galois::for_each is suitable to implement push-style algorithms.
galois::for_each uses galois::UserContext, a per-thread object, to track conflicts and new work. To insert new work items into the worklist, call galois::UserContext::push. To detect conflicts, galois::UserContext maintains a linked list of acquired items. Each sharable object, e.g. graph nodes, has a lock, which is automatically acquired when getData(), edge_begin(), edge_end(), edges(), etc. are called. A conflict is detected by the Galois runtime when the lock acquisition fails. Locks are released when aborting or finishing an iteration. Since Galois assumes cautious operators, i.e. no writes to user state before acquiring all locks, there is no need to rollback user state when aborting an iteration.
galois::for_each expects the following inputs:
Below is the code snippet of using galois::for_each with conflict detection to implement our running example. It uses a push-style algorithm: Each node adds each of its edge's weight to the corresponding neighbor. Note that the operator code is written as in sequential code; and that the operator expects auto& ctx, a reference to galois::UserContext.
The code snippet below shows how to let an operator, instead of galois::for_each, take care of synchronization. Conflict detection is turned off in this case. Since there is no new work generated and the operator synchronizes node data, the same code can be implemented with galois::do_all as well, which is also shown in this example.
See lonestar/tutorial_examples/GraphTraversalPushOperator.cpp for the full examples.
So far, we addressed only topology-driven algorithms, e.g. the same computation is done by all graph nodes. To implement data-driven algorithms, two more constructs are needed: (1) a worklist to track active elements, and (2) a scheduler to decide which active elements to work on first. New work items can be inserted to a worklist by calling galois::UserContext::push. This section focuses on the schedulers supported by Galois.
Galois supports a variety of scheduling policies, all of them are in the namespace galois::worklists. Example scheduling policies are galois::worklists::FIFO (approximate), galois::worklists::LIFO (approximate), galois::worklists::ChunkFIFO, galois::worklists::ChunkLIFO, galois::worklists::PerSocketChunkFIFO, galois::worklists::PerSocketChunkLIFO, galois::worklists::PerThreadChunkFIFO, galois::worklists::PerThreadChunkLIFO, and galois::worklists::OrderedByIntegerMetric. The default scheduler is galois::worklists::PerSocketChunkFIFO with a chunk size 32.
galois::worklists::OrderedByIntegerMetric can be used to implement a user-defined soft priority, a hint for the Galois runtime to schedule active elements where priority inversion will not result in incorrect answers or deadlocks. It needs an indexer function to map work items to an integer (priority). Each bin corresponds to a priority level and is itself a worklist, e.g. galois::worklists::PerSocketChunkLIFO with a chunk size 16.
Let us use the single-source shortest path (SSSP) problem to illustrate the implementation of data-driven algorithms using Galois. Given (1) an edge-weighted graph G with no negative-weight cycles, and (2) a source node s; the SSSP problem asks for the shortest distance of every node n in G from s. Initially, s has distance 0 from itself, and all other nodes have a distance of infinity from s.
Here is the operator code common to all push-style SSSP algorithms:
And here is the code to declare worklists. Note how OBIM is declared with an indexer, e.g. reqIndexer, and another worklist, e.g. PerSocketChunkLIFO<16>.
Finally, here is the code for implementing data-driven algorithms. Initial active elements, e.g. the source node in this example, are passed to galois::iterate as an initializer list. Schedules are passed as options to galois::for_each. Note that OBIM expects an indexer instance for its construction.
The full example is available at lonestar/tutorial_examples/SSSPPushSimple.cpp
galois::do_all and galois::for_each assume that the operator allows the loop iterations to be computed in any order, which may give legal yet different results non-deterministically. When it is important to have deterministic results, the deterministic loop iterator comes to the rescue: it executes the operator in rounds, and in each round, it deterministically chooses a conflict-free subset of currently active elements to process. In this way, the Galois deterministic loop iterator can produce the same answer even on different platforms, which we call "portable determinism".
Galois' deterministic loop iterator can be launched on-demand and parameter-less by passing galois::wl< galois::worklists::Deterministic <> > to galois::for_each. Use galois::UserContext::cautiousPoint to signal the cautious point in the operator if necessary. Below is an example of using the deterministic loop executor for SSSP:
An algorithm can benefit from parallelization only if it has a lot of parallelism. Galois provides the ParaMeter loop iterator to help algorithm designers find out the amount of parallelism in their algorithms. This parallelism, of course, depends on input-data. The ParaMeter loop iterator executes the operator in rounds and keeps track of statistics of parallelism for each round.
To launch Galois' ParaMeter loop iterator, pass galois::wl< galois::worklists::ParaMeter <> > to galois::for_each. Below is an example of using ParaMeter loop executor for SSSP:
Runs using the ParaMeter loop iterator will generate a parallelism profile as a csv file whose prefix is "ParaMeter-Stats-". A sample ParaMeter csv output looks like the following:
LOOPNAME, STEP, PARALLELISM, WORKLIST_SIZE, NEIGHBORHOOD_SIZE
sssp_ParaMeter, 0, 1, 1, 4
sssp_ParaMeter, 1, 1, 3, 4
sssp_ParaMeter, 2, 2, 4, 4
sssp_ParaMeter, 3, 2, 2, 6
sssp_ParaMeter, 4, 1, 2, 4
sssp_ParaMeter, 5, 2, 3, 9
sssp_ParaMeter, 6, 2, 6, 6
sssp_ParaMeter, 7, 3, 6, 12
sssp_ParaMeter, 8, 5, 9, 18
sssp_ParaMeter, 9, 7, 12, 27
sssp_ParaMeter, 10, 8, 18, 28
...
The parallelism profile should be interpreted as follows:
Upon termination, Galois apps will output statistics in csv format, similar to the following:
STAT_TYPE, REGION, CATEGORY, TOTAL_TYPE, TOTAL
STAT, for_each_1, Iterations, TSUM, 9028387
STAT, for_each_1, Time, TMAX, 1663
STAT, for_each_1, Commits, TSUM, 9000000
STAT, for_each_1, Pushes, TSUM, 0
STAT, for_each_1, Conflicts, TSUM, 28387
The first row is the header of the csv output. REGION tells you which parallel loop the statistics are related to. For example, "for_each_1" refers to the galois::for_each which has an option of galois::loopname("for_each_1").
CATEGORY specifies what is being reported for the parallel region. For galois::for_each loops, the following five statistics are reported:
For galois::do_all loops, only time and iterations are reported, since there are no conflicts and pushes in galois::do_all loops.
TOTAL_TYPE tells you how the statistics are derived. TSUM means that the value is the sum of all threads' contributions; TMAX means it is the maximum among all threads for this statistic. TOTAL_TYPE is usually a reduction operation.
If your application requires modifying the graph topology, e.g. as in Delaunay mesh refinement, you need galois::graphs::MorphGraph. galois::graphs::MorphGraph supports all the functionalities in galois::graphs::LC_CSR_Graph except for size(), reporting the number of nodes in a graph; and sizeEdges(), reporting the number of edges in a graph. Additionally, galois::graphs::MorphGraph provides the following APIs to modify the graph topology:
Let us use galois::graphs::MorphGraph to construct and represent a two-dimensional torus. To define a galois::graphs::MorphGraph, you must provide as template parameters NodeTy, the type of node data; EdgeTy, the type of edge data; and a Boolean value indicating whether or not this is a directed graph. The following code snippet shows an example of defining a galois::graphs::MorphGraph. See galois::graphs::MorphGraph for details about other optional template parameters.
The following code snippet shows how to add nodes and edges to a galois::graphs::MorphGraph. Note that you need to create nodes first, then add the nodes to a galois::graphs::MorphGraph, and finally add edges in between the nodes.
See the full example at lonestar/tutorial_examples/TorusConstruction.cpp
Performance tuning is required to make a parallel program fast and scalable. Readers should keep the following points in mind when tuning performance:
We have walked through the key user-level Galois constructs for writing a C++ parallel program. For details about the aforementioned constructs, library-level Galois constructs, and performance tuning, please refer to Manual.