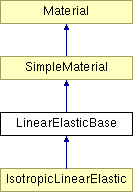
LinearElasticBase Class Reference
Linear Elastic constitutive behavior. More...
#include <Material.h>
Public Member Functions | |
| LinearElasticBase (double irho=0) | |
| virtual | ~LinearElasticBase () |
| LinearElasticBase (const LinearElasticBase &NewMat) | |
| virtual LinearElasticBase * | clone () const =0 |
| bool | getConstitutiveResponse (const std::vector< double > &strain, std::vector< double > &stress, std::vector< double > &tangents, const ConstRespMode &mode) const |
| Returns the constitutive response of the material. | |
| const std::string | getMaterialName () const |
| returns a string with the name of the material | |
Protected Member Functions | |
| virtual const double | getModuli (int i1, int i2, int i3, int i4) const =0 |
Detailed Description
Linear Elastic constitutive behavior.
This is an abstract class that provides the constitutive response of a linear elastic material. However, it does not store the moduli, leaving that task for derived classes. In this way, we have the flexibility to handle cases in which the material has different types of anisotropy or under stress.
Constructor & Destructor Documentation
| LinearElasticBase::LinearElasticBase | ( | double | irho = 0 |
) | [inline] |
| virtual LinearElasticBase::~LinearElasticBase | ( | ) | [inline, virtual] |
| LinearElasticBase::LinearElasticBase | ( | const LinearElasticBase & | NewMat | ) | [inline] |
Member Function Documentation
| virtual LinearElasticBase* LinearElasticBase::clone | ( | ) | const [pure virtual] |
Implements SimpleMaterial.
Implemented in IsotropicLinearElastic.
| bool LinearElasticBase::getConstitutiveResponse | ( | const std::vector< double > & | strain, | |
| std::vector< double > & | stress, | |||
| std::vector< double > & | tangents, | |||
| const ConstRespMode & | mode | |||
| ) | const [virtual] |
Returns the constitutive response of the material.
Given the local strain, it returns the local stress, and if requested, the constitutive tangents.
More precisely:
The strain is assumed to be a 3x3 second-order tensor 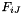 .
.
The stress is assumed to be a 3x3 second-order tensor 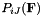 .
.
The constitutive tangents are a 3x3x3x3 fourth-order tensor
![\[ A_{iJkL} = \frac{\partial P_{iJ}}{\partial F_{kL}} \]](form_69.png)
- Parameters:
-
strain strain tensor, input stress array where the stress tensor is returned tangents array where the constitutive tangents are returned. If not provided, not computed. mode tells whether to compute tangents vector or skip it
- See also:
- ConstRespMode
If cannot compute the constitutive relation for some reason, for example a negative determinant in the strain, it returns false. If successful, returns true.
Implements SimpleMaterial.
| const std::string LinearElasticBase::getMaterialName | ( | ) | const [inline, virtual] |
returns a string with the name of the material
Implements SimpleMaterial.
Reimplemented in IsotropicLinearElastic.
| virtual const double LinearElasticBase::getModuli | ( | int | i1, | |
| int | i2, | |||
| int | i3, | |||
| int | i4 | |||
| ) | const [protected, pure virtual] |
Implemented in IsotropicLinearElastic.
The documentation for this class was generated from the following files:
 1.6.3
1.6.3