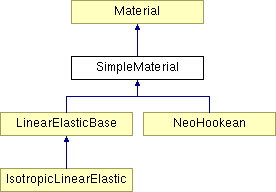
SimpleMaterial Class Reference

Material whose thermodynamic state depends only on the local strain. More...

#include <Material.h>

Inheritance diagram for SimpleMaterial:

List of all members.

Public Types
enum	ConstRespMode { COMPUTE_TANGENTS, SKIP_TANGENTS }
	for use with getConstitutiveResponse optional to compute the tangents or skip the computation More...
Public Member Functions
	SimpleMaterial (double rhoInput=0)
virtual	~SimpleMaterial ()
	SimpleMaterial (const SimpleMaterial &SM)
	Copy constructor.
virtual SimpleMaterial *	clone () const =0
virtual bool	getConstitutiveResponse (const std::vector< double > &strain, std::vector< double > &stress, std::vector< double > &tangents, const ConstRespMode &mode) const =0
	Returns the constitutive response of the material.
double	getDensityInReference () const
	Returns the (uniform) density of the reference configuration.
bool	getLocalMaterialDensity (const std::vector< double > *strain, double &LocDensity) const
	Returns the local density that is a function of only the strain.
virtual const std::string	getMaterialName () const =0
	returns a string with the name of the material
virtual double	getSoundSpeed (void) const =0
Static Public Member Functions
static bool	consistencyTest (const SimpleMaterial &Smat)
	Consistency test Checks that the tangets are in fact the derivatives of the stress with respect to the strain.
Static Public Attributes
static const double	EPS = 1.e-6
	Some constants collected together here.
static const double	PERT = 1.e-1
static const double	DET_MIN = 1.e-10
static const size_t	MAT_SIZE = 9
static const size_t	NDF = 3
static const size_t	NDM = 3
static const double	I_MAT [MAT_SIZE] = { 1., 0., 0., 0., 1., 0., 0., 0., 1. }
Private Attributes
double	RefRho

---

Detailed Description

Material whose thermodynamic state depends only on the local strain.

Simple materials are those for which the stress depends only on the strain. Assumes a homogeneous density in the reference configuration.

Convention:
Any 3x3 second-order tensor 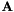is represented by a 2x2 matrix with components ordered in an array 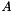as 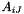=A[i*3+J].
Any 3x3x3x3 fourth-order tensor 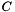is represented by a 3x3x3x3 matrix with components ordered in an array 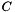as 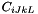=C[i*27+J*9+k*3+l].

---

Member Enumeration Documentation

enum SimpleMaterial::ConstRespMode

for use with getConstitutiveResponse optional to compute the tangents or skip the computation

Enumerator:

COMPUTE_TANGENTS
SKIP_TANGENTS

---

Constructor & Destructor Documentation

SimpleMaterial::SimpleMaterial

(

double

rhoInput = 0

)

[inline]

Parameters:

rhoInput

Density in reference configuration. If not provided, assumed to be zero.

virtual SimpleMaterial::~SimpleMaterial

(

)

[inline, virtual]

SimpleMaterial::SimpleMaterial

(

const SimpleMaterial &

SM

)

[inline]

Copy constructor.

Parameters:

SM

SimpleMaterial object to be copied.

---

Member Function Documentation

virtual SimpleMaterial* SimpleMaterial::clone

(

)

const [pure virtual]

Implemented in NeoHookean, LinearElasticBase, and IsotropicLinearElastic.

bool SimpleMaterial::consistencyTest

(

const SimpleMaterial &

Smat

)

[static]

Consistency test
Checks that the tangets are in fact the derivatives of the stress with respect to the strain.

virtual bool SimpleMaterial::getConstitutiveResponse	(	const std::vector< double > &	strain,
		std::vector< double > &	stress,
		std::vector< double > &	tangents,
		const ConstRespMode &	mode
	)			const [pure virtual]

Returns the constitutive response of the material.

Given the local strain, it returns the local stress, and if requested, the constitutive tangents.

More precisely:
The strain is assumed to be a 3x3 second-order tensor .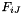
The stress is assumed to be a 3x3 second-order tensor .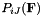
The constitutive tangents are a 3x3x3x3 fourth-order tensor

Parameters:

	strain	strain tensor, input
	stress	array where the stress tensor is returned
	tangents	array where the constitutive tangents are returned. If not provided, not computed.
	mode	tells whether to compute tangents vector or skip it

See also:

ConstRespMode

If cannot compute the constitutive relation for some reason, for example a negative determinant in the strain, it returns false. If successful, returns true.

Implemented in NeoHookean, and LinearElasticBase.

double SimpleMaterial::getDensityInReference

(

)

const [inline]

Returns the (uniform) density of the reference configuration.

bool SimpleMaterial::getLocalMaterialDensity	(	const std::vector< double > *	strain,
		double &	LocDensity
	)			const [inline]

Returns the local density that is a function of only the strain.

The density is computed as

where 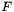is the deformation gradient (as described above).
Returns true if the computation went well and false otherwise.

Parameters:

	strain	Deformation gradient.
	LocDensity	Computed local density.

virtual const std::string SimpleMaterial::getMaterialName

(

)

const [pure virtual]

returns a string with the name of the material

Implemented in NeoHookean, LinearElasticBase, and IsotropicLinearElastic.

virtual double SimpleMaterial::getSoundSpeed

(

void

)

const [pure virtual]

Returns:

speed of sound

Implemented in NeoHookean, and IsotropicLinearElastic.

---

Member Data Documentation

const double SimpleMaterial::DET_MIN = 1.e-10 [static]

const double SimpleMaterial::EPS = 1.e-6 [static]

Some constants collected together here.

const double SimpleMaterial::I_MAT = { 1., 0., 0., 0., 1., 0., 0., 0., 1. } [static]

const size_t SimpleMaterial::MAT_SIZE = 9 [static]

const size_t SimpleMaterial::NDF = 3 [static]

const size_t SimpleMaterial::NDM = 3 [static]

const double SimpleMaterial::PERT = 1.e-1 [static]

double SimpleMaterial::RefRho [private]

---

The documentation for this class was generated from the following files:

• Material.h
• Material.cpp