Betweenness Centrality
Application Description
This benchmark computes the betweenness centrality of each node in a network, a metric that captures the importance of each individual node in the overall network structure. Betweenness centrality is a shortest path enumeration-based metric. Informally, it is defined as follows. Let G=(V,E) be a graph and let (s,t) be a fixed pair of graph nodes.The betweenness score of a node (u) is the percentage of shortest paths between (s) and (t) that include (u). The betweenness centrality of (u) is the sum of its betweenness scores for all possible pairs of (s) and (t) in the graph. The benchmark takes as input a directed graph and returns the betweenness centrality value of a number of nodes.
Implementation Details
We have 2 implementations: one that calculates BC contributions one at a time, and another that is provably communication efficient and calculates BC contributions for many nodes at. We detail the former below. Then, we briefly summarize the latter; details can be found in our paper [1].
The first implementation of betweenness-centrality in the distributed setting is called Synchronous Brandes-BC (see the shared memory betweenness-centrality page for more information on Brandes's algorithm). We present a high-level description of how the algorithm works below.
Abstractly, there is still a forward phase and a backward phase: the forward phase gets shortest paths counts, distances, and a DAG of the shortest paths from the source being operated on, and the backward phase propagates dependency values backwards from the leaves of the DAG. Our implementation splits the 2 phases into 2 passes. (A "pass" in this case may make multiple sweeps over the graph; we refer to a pass as a sub-phase, in some sense.)
In the forward phase, we have a pass that first performs BFS on the entire graph to find distances from the source and number of shortest paths.
In the backward phase, we have a single pass that will start from the leaves of the DAG and propagate the dependencies up to the root of the DAG. The order of propagation is known via the distance on each node which designates the level of the node on the DAT.
Each of the passes above has synchronization that reconciles distances, counts of shortest paths, and dependency calculations, among other things.
| 1 2 3 4 5 6 7 | Graph g = /* read input graph */; foreach (Node n in g) { InitializeSource(n, g) // Forward Phase BFS(g) // Backward Phase DependencyPropagation(g) } |
Figure 1: Pseudocode for Steps of Synchronous Brandes-BC
BFS
This pass is a regular level by level BFS calculation (see our page on distributed BFS to get an idea of what is being done). The algorithm locally counts the number of shortest paths as well. At the end of the BFS step, a synchronization step occurs to synchronize shortest path counts across all nodes.
Dependency Propagation
Once the number of shortest paths is found, we can proceed to the backward phase of Brandes's algorithm where dependencies (calculated from the number of shortest paths and dependencies of successor nodes) are propagated backwards along the DAG. We work backwards from the leaves of the DAG: in each BSP round, we move up a level of a DAG and propagate it backward. These levels are guaranteed to have finalized dependency values as all of its children's dependencies will have been finalized in previous BSP rounds. In addition, we know exactly which nodes are predecessors in the DAG via the distances on each node: a predecessor of some node is its own distance subtracted by 1. Dependencies are synchronized at the end of every BSP round on the level being operated on.
Min Rounds BC
Our second implementation is called Min Rounds Betweenness Centrality. It calculates BC contributions for multiple vertices at one time which reduces the amount of communication rounds overall. It leverages an insight proved in the paper [1] that allows the algorithm to know exactly when a value is ready to be communicated to other machines: this makes it so communication only occurs when it is necessary, further reducing communication overhead. The paper [1] gives more details on the implementation as well as other optimizations.
Performance
The figure below shows the scaling of Synchronous Brandes BC and Min Rounds BC on Stampede2's Skylake cluster which is connected through Intel Omni-Path Architecture (peak bandwidth of 100Gbps). Each node has 2 Intel Xeon Platinum 8160 “Skylake” CPUs with 24 cores per CPU and 192GB DDR4 RAM. The graphs are for clueweb12 and gsh15, two of the largest publicly available web crawls. Both calculate BC using a subset of all sources in the graph as doing all sources would take a prohibitive amount of time.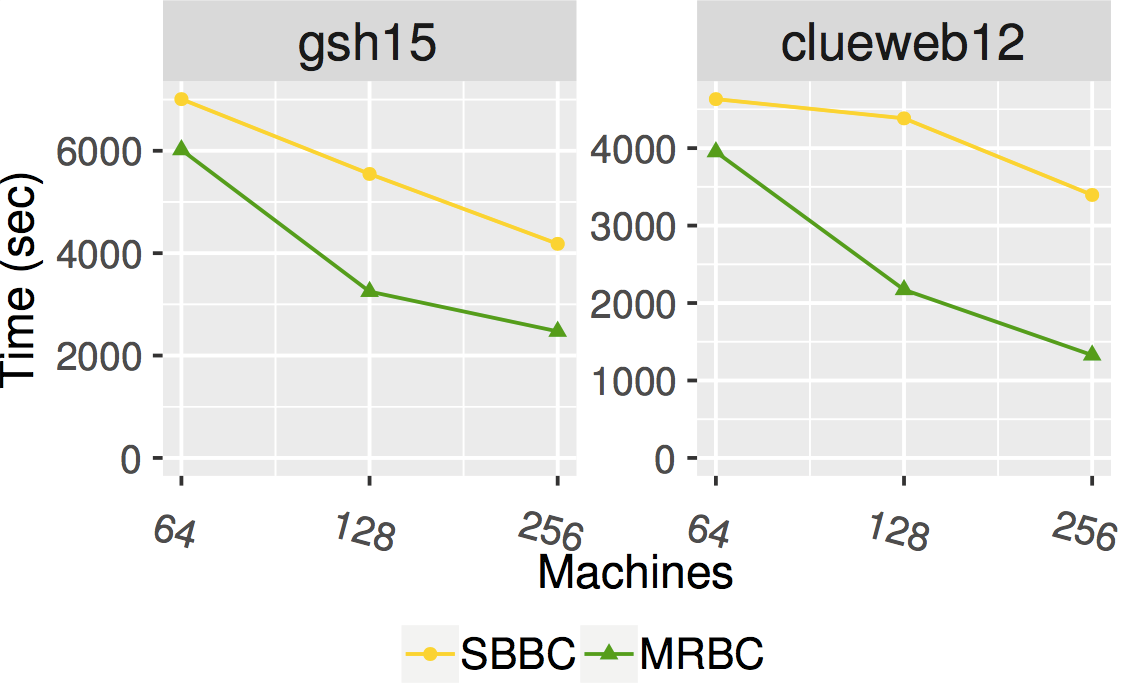
[1] Loc Hoang, Matteo Pontecorvi, Roshan Dathathri, Gurbinder Gill, Bozhi You, Keshav Pingali, and Vijaya Ramachandran. A Round-Efficient Distributed Betweenness Centrality Algorithm. PPoPP 2019.
