SPRoute
Application Description
SPRoute performs global routing on a circuit of ISPD2008 contest format.
Global routing first partitions the chip area into global cells (Gcells) and then generates a grid graph. It then construct routes on the grid graph to provide a preferred routing region for detailed routing. This is illustrated in Figure 1.
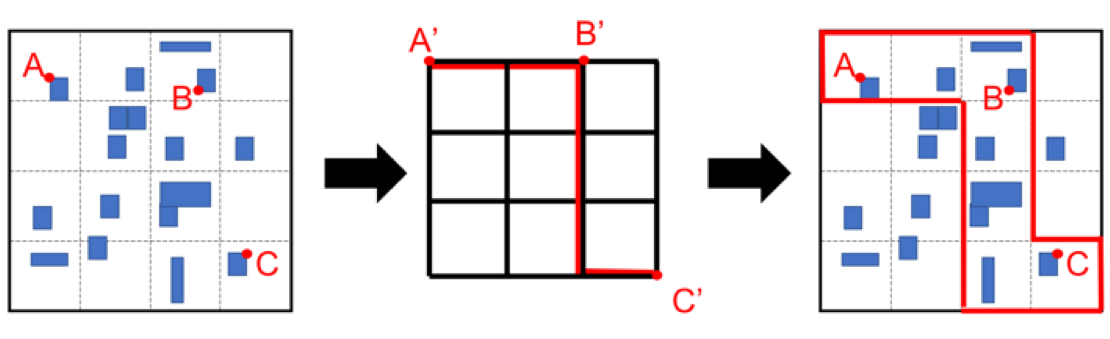
There are three attributes on the edge: capacity, usage and overflow.
Capacity: the maximum number of wires that can use an edge
Usage: the number of wires using the edge currently
Overflow: the number of wires exceeding the capacity
The global routing problem is: for every input net, find a route that connects the pins of the net on the grid graph. The first objective is to minimize the total overflow of all edges. The second objective is to minimize the wire length. The cost of vias is also considered in multi-layer designs.
Algorithm
SPRoute is based on FastRoute 4.1 and consists of four stages: tree decomposition, pattern routing, maze routing and layer assignment. Maze routing is the most time-consuming stage. It performs ripup and reroute negotiation-based maze routing on each net until the overflow converges to zero. There are three loops as parallelization candidates in maze routing (line 1, 2, 6 in Figure 2). SPRoute parallelizes the outer-most loop (Net-level parallelism) and inner-most loop (fine-grain parallelism).
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | INPUT: A set of nets N and a grid graph G(V, E) for each net n in N do #net-level parallelism for each two-pin net e of n do if ripup check(G, e) then ripup(G, e) WL.push(e.source nodes) while !W L.empty() do #fine-grain parallelism node = W L.pop() neighbors = maze expand(G, node) WL.push(neighbors) end while trace_back(G, e) adjust_tree(n, e) end if end for end for |
Figure 2: Pseudocode for maze routing
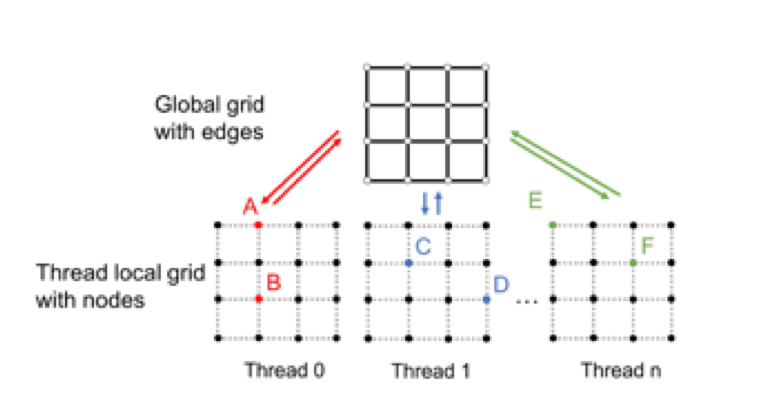
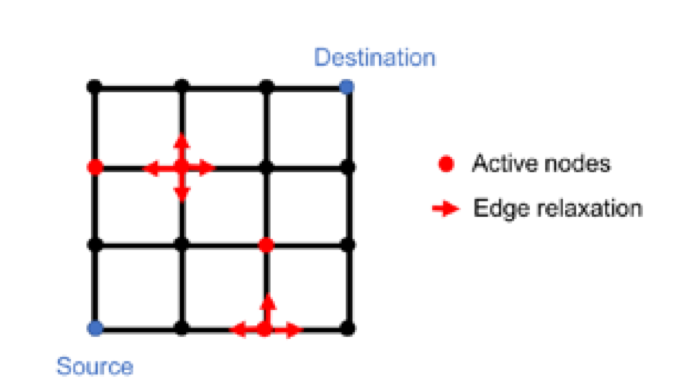
To achieve good speedup, SPRoute first parallelize the outer-most loop and does not apply locking to the routing region (Figure 3). Threads may read stale value from global grid because there is no locking. This results in live lock and makes overflow unable to converge to zero. SPRoute then reduces the number of threads to reduce the probability of live lock. If such phenomenon still exists, SPRoute switches to fine-grain parallelism to guarantee convergence (Figure 4). Figure 5 illustrates this hybrid scheme.
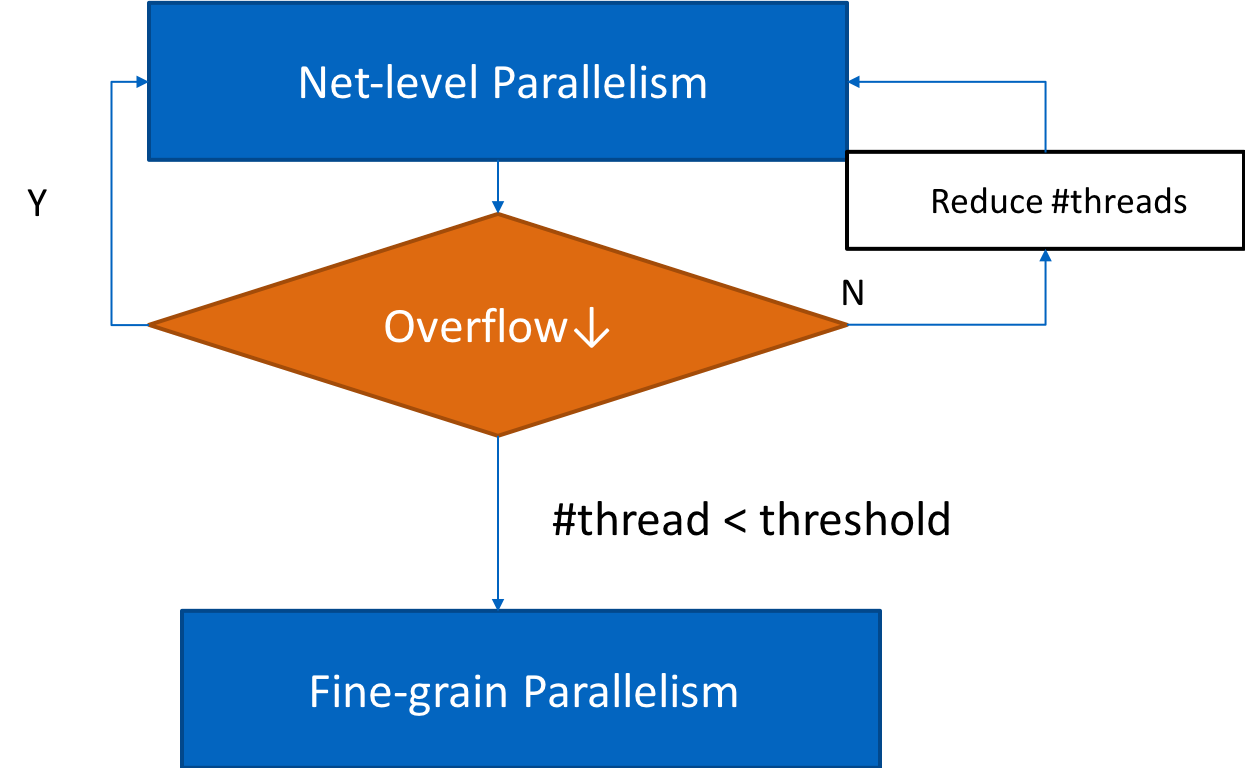
Performance
Compared to FastRoute 4.1, SPRoute achieves an average speedup of 11.0 on overflow-free cases and 3.1 on hard-to-route cases with some quality reduction on ISPD2008 benchmarks.
| Num. of cases | Average Speedup | Quality Reduction | |
|---|---|---|---|
| Overflow-free cases | 11 | 11.0 | Wirelength 0.6% |
| Hard-to-route cases | 4 | 3.1 | Overflow 7% |
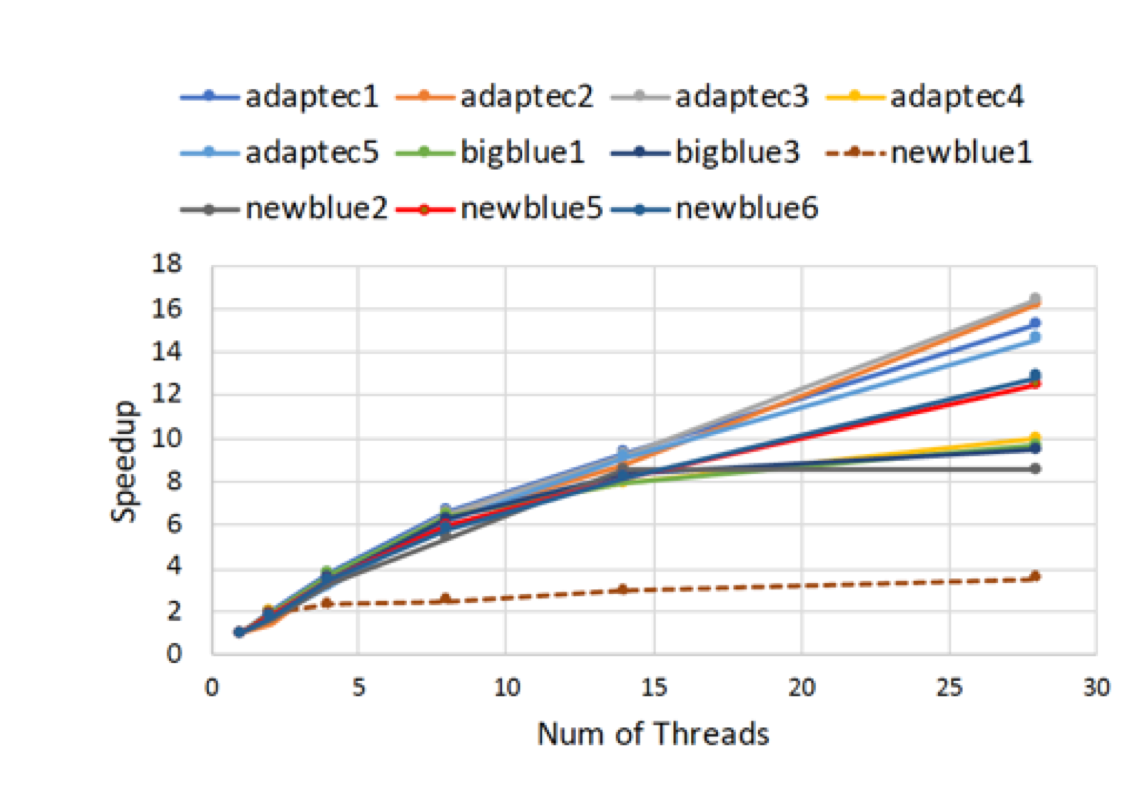
The following figure shows the scalability of SPRoute on overflow-free cases.
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
