Maximum Cardinality Bipartite Matching
Application Description
Given a graph G, a matching M is a subset of edges where no two edges share an endpoint. The cardinality |M| of M is the number of edges in M . Given an unweighted bipartite graph G = (V, E) V = (A, B), the maximum cardinality bipartite matching problem is to find a matching with maximum cardinality.
Algorithm
Algorithms to solve this problem try to extend existing matchings by finding augmenting paths. When there are no more augmenting paths, the matching is a maximum matching.
The Ford-Fulkerson algorithm [1] visits each node in A trying to find an augmenting path at each. It has complexity O(|V||E|). The Alt-Blum-Mehlhorn-Paul (ABMP) algorithm [1] tries to find the shortest augmenting path first. After all the augmenting paths of less than a particular length are found or the number of unmatched nodes is reduced to a particular size, the algorithm applies the Ford-Fulkerson algorithm to complete the matching. The ABMP algorithm has complexity O(|E|sqrt(|V|)).
This benchmark implements the Alt-Blum-Mehlhorn-Paul algorithm.
[1] K. Mehlhorn and S. Naeher. LEDA: A Platform for Combinatorial and Geometric Computing. Cambridge University Press, 1999.
Data Structures
There are two key data structures used in this algorithm:
- Priority Scheduler
- The ABMP algorithm uses priority on tasks to find the shortest augmenting paths first.
- Directed Graph
- The algorithm successively reads and updates a graph.
Performance
Figure 3 and Figure 4 show the execution time in seconds and self-relative speedup (speedup with respect to the single thread performance), respectively, of this algorithm
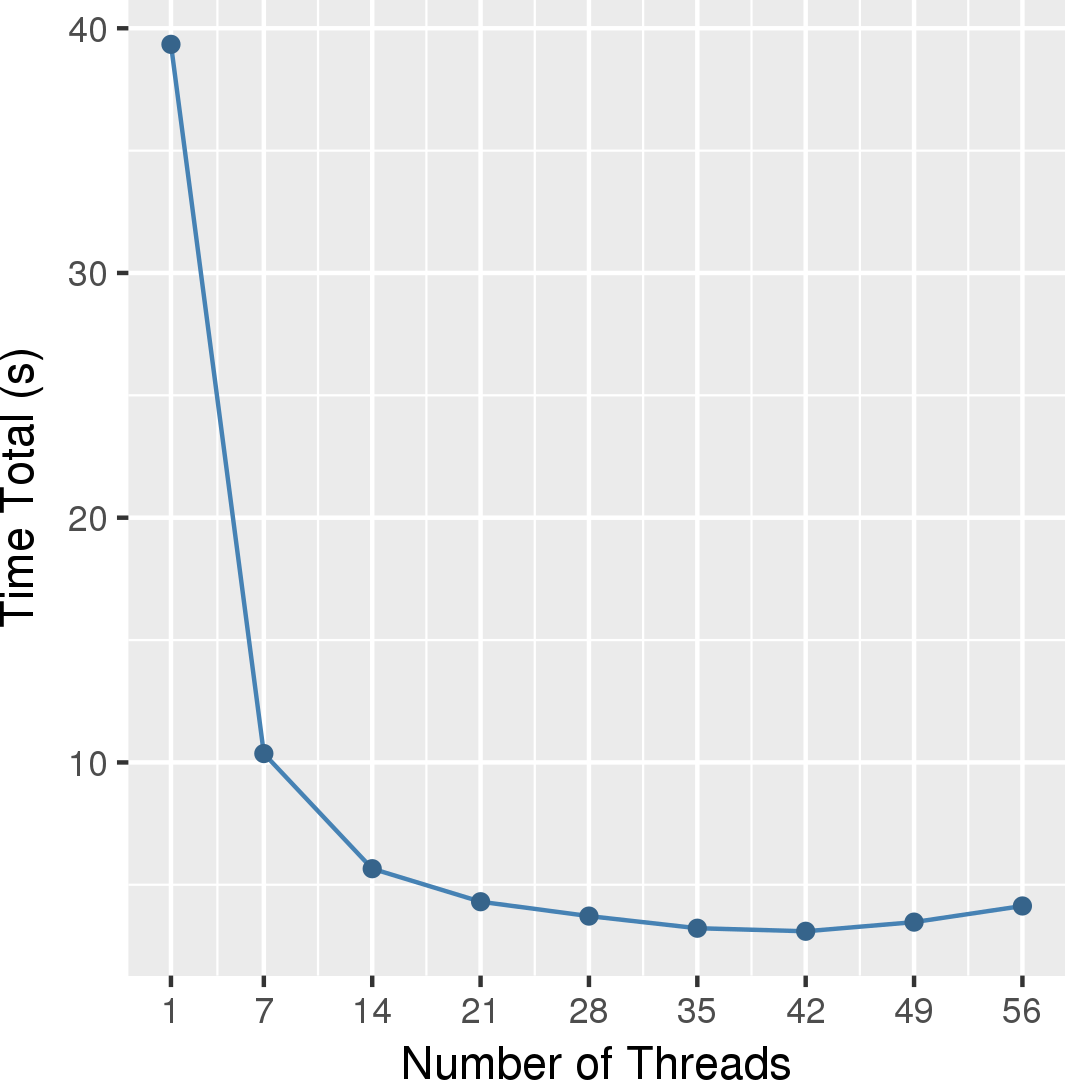
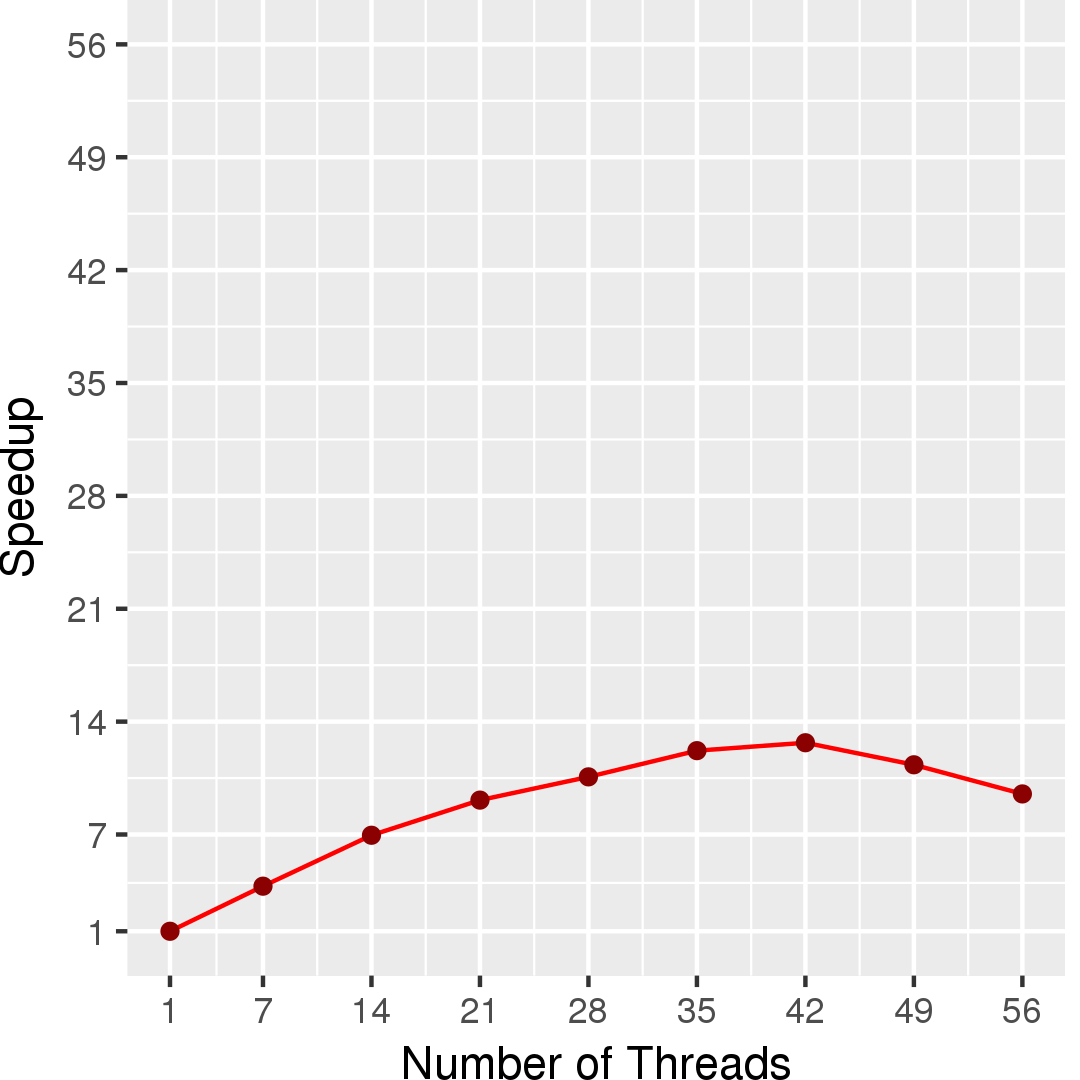
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
