PageRank
Application Description
PageRank is a key technique in web mining to rank the importance of web pages. In PageRank, each web page is assigned a numerical weight to begin with, and the algorithm tries to estimate the importance of the web page relative to other web pages in the hyperlinked set of pages. The key assumption is that more important web pages are likely to receive more links from other websites. More details about the problem and different solutions can be found in [1, 2].
[1] https://en.wikipedia.org/wiki/PageRank
[2] Whang et al. Scalable Data-driven PageRank: Algorithms, System Issues, and Lessons Learned. European Conference on Parallel Processing, 2015.
This benchmark computes the PageRank of the nodes for a given input graph using both a push-style and a pull-style residual-based algorithm. Both the algorithms take as input a graph, and some constant parameters that are used in the computation. The algorithmic parameters are the following:
- ALPHA: ALPHA represents the damping factor, which is the probability that a web surfer will continue browsing by clicking on the linked pages. The damping factor is generally set to 0.85 in the literature.
- TOLERANCE: It represents a bound on the error in the computation.
- MAX_ITER: The number of iterations to repeat the PageRank computation.
Pull-style Residual Algorithm
In the pull-style algorithm, each node n maintains three pieces of information: its own PageRank value, the residual information that is contributed by n's incoming neighbors, and the delta which represents n's new contribution to the PageRank of its outgoing neighbors in the next iteration. In lines 24-35, a node n updates its own PageRank with the residual from the last iteration and computes its new contribution to its outgoing neighbors scaled by the damping factor (delta[src]). In lines 37-47, each node accumulates the contributions from all of its incoming neighbors into its residual which might be used (e.g., if the residual is greater than the TOLERANCE) in the next iteration to update its PageRank.
The termination condition of the algorithm is specified using two conditions. The first condition checks whether any node has updated its PageRank information in the current iteration (tracked by the variable changed). The computation can be terminated if no node has updated its PageRank. Please note that these updates depend on the value of TOLERANCE. The second condition checks if the maximum number of iterations have been reached.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 | float ALPHA = 0.85; // damping factor float TOLERANCE = 1.0e-3; int MAX_ITER = 1000; Graph g = /* read input */; float pagerank[] = new float[g.size()]; float delta[] = new float[g.size()]; // Track incremental contributions from incoming neighbors float residual[] = new float[g.size()]; // Initialize the data structures foreach(Node n : g.getNodes()) { pagerank[n] = 0; delta[n] = 0; residual[n] = 1 - ALPHA; // Own contribution in the first iteration } int iterations = 0; while (true) { bool changed = false; foreach(Node src : g.getNodes()) { delta[src] = 0; if (residual[src] > TOLERANCE) { float oldResidual = residual[src]; pagerank[src] += oldResidual; residual[src] = 0.0; if (src.outdegree > 0) { delta[src] = oldResidual * ALPHA / src.outdegree; changed = true; } } } foreach(Node src : g.getNodes()) { float sum = 0; for (Node n : g.getIncomingNeighbors(src)) { if (delta[n] > 0) { sum += delta[n]; } } if (sum > 0) { residual[src] = sum; } } iterations++; if (iterations >= MAX_ITER || !changed) { // termination condition break; } } // end while (true) |
Figure 1: Pseudocode for the pull-style residual-based PageRank algorithm.
Data Structures
The following are the key data structures used in this implementation:- Array
- It represents an array of values with each index mapping to a node in the graph. The implementation uses a structure of arrays (separate arrays are used for tracking the PageRank, residual, and the delta values) instead of an array of structures for better data locality.
- Graph
- A labeled, directed graph, in which every node stores its excess and height, and every edge stores its maximum and current flows.
Performance
Figure 2 and Figure 3 show the execution time in seconds and self-relative speedup (speedup with respect to the single thread performance), respectively, of the pull-style residual algorithm running on the Twitter graph.
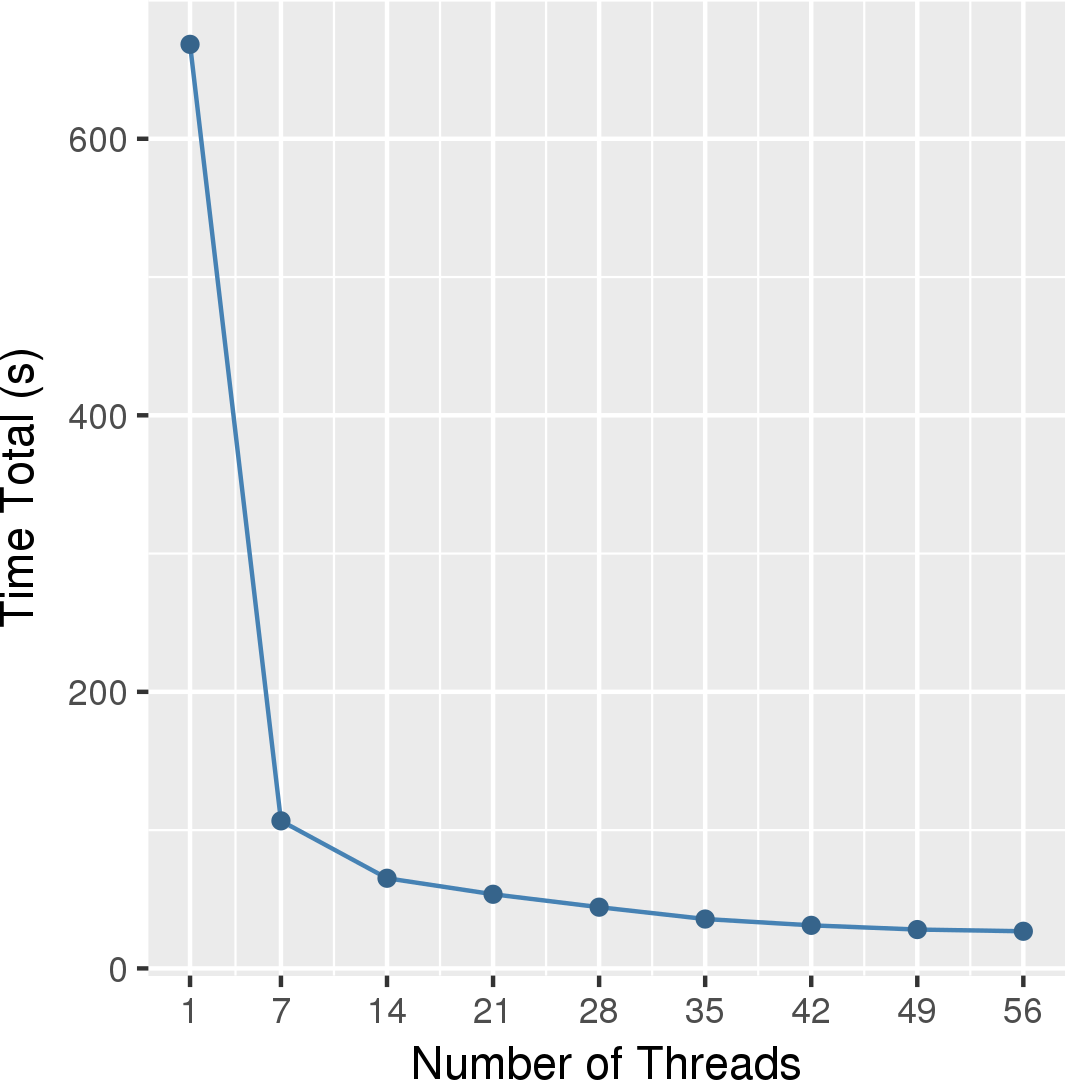
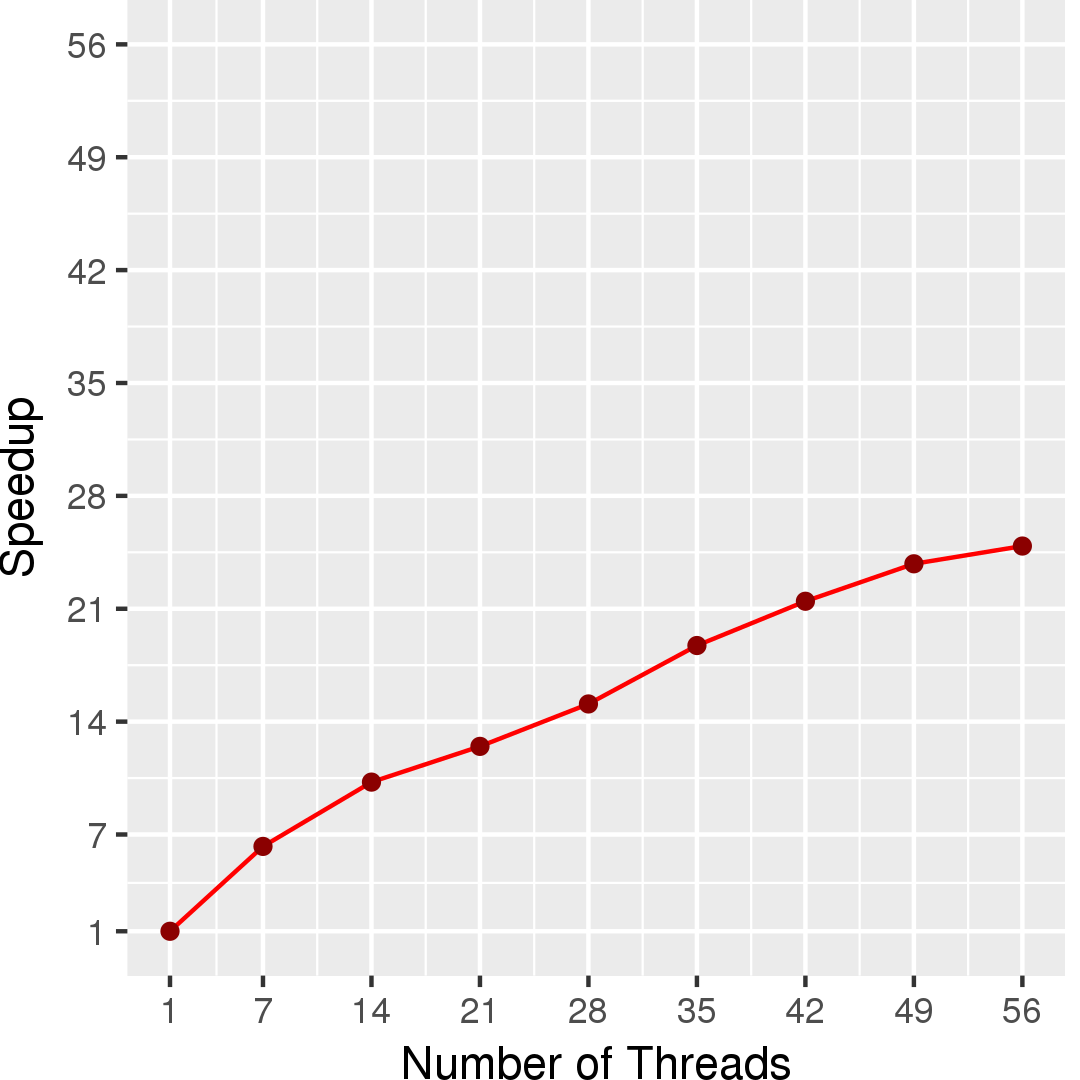
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
