Connected Components
Application Description
A connected component of an undirected graph is a subgraph in which there is a path between any two nodes. A node with no edges is itself a connected component. (Wikipedia)
Algorithms
Algorithms for connected components are based on either union-find or label-propagation.
- The Union-Find algorithm is based on pointer jumping. Each node has a pointer to its representative, initially set to itself. If two nodes a and b are connected by an edge e, then the union operation updates representatives of a and b to be the same. The find operation updates the representative of a node to be one of its ancestors in the representative relation.
- In Label Propagation, each node is given a unique label initially, and then labels are propagated through the graph until all the nodes in the same component have the same label.
An optimization for union-find is called Afforest, an algorithm with subgraph sampling, where union-find is first performed on a few samples of neighborhoods of all vertices (Vertex Neighbor Sampling) and then on the rest of neighborhoods of only those vertices not belonging to the largest component approximated by another sampling process (Largest Component Skipping).
M. Sutton, T. Ben-Nun and A. Barak, "Optimizing Parallel Graph Connectivity Computation via Subgraph Sampling," 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Vancouver, BC, 2018, pp. 12-21, doi: 10.1109/IPDPS.2018.00012.
The Connected Components application implements 7 algorithms: 1-9 are variants of union-find, and 10 is label propagation.
- Serial: Serial pointer-jumping implementation.
- Synchronous: Bulk synchronous data-driven implementation. Alternatively execute on two worklists.
- Async: asynchronous topology-driven implementation. Work unit is a node.
- BlockedAsync: asynchronous topology-driven implementation with NUMA-aware optimization. Work unit is a node.
- EdgeAsync: asynchronous topology-driven. Work unit is an edge.
- EdgetiledAsync (default): asynchronous topology-driven. Work unit is an edge tile.
-
Afforest: data-driven implementation with Afforest subgraph sampling algorithm. Work unit is a node.
- EdgeAfforest: data-driven implementation with subgraph sampling. Work unit is an edge.
- EdgetiledAfforest: data-driven implementation with subgraph sampling. Work unit is an edge tile.
- LabelProp: Label propagation implementation.
Note that Connected Components only accepts a symmetric input graph.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | Graph g = /*input graph*/ foreach (Node src : g) { foreach (Node dst : src.getNeighbors()) { if(src.id > dst.id) continue; while(true) { src.findAndCompress(); //update representative to be one of its ancestors dst.findAndCompress(); if(src.representative == dst.representative) break; Union(src, dst); //update representative to be the same } } } |
Figure 1: Pseudocode for Pointer Jumping(1-6) algorithm.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | Graph g = /*input graph*/ const int PARAM_VNS = /*number of sampled edges (per vertex) for Vertex Neighbors Sampling*/ const int PARAM_LCS = /*number of sampled vertices for Largest Component Skipping*/ foreach (Node src : g) { foreach (Node dst : src.getSampledNeighbors(PARAM_VNS)) { /*pointer jumping operations as demostrated in Figure 1*/ } } Node r = sampLgstComp(g, PARAM_LCS); //approximate the largest component via PARAM_LCS times sampling and return the representative of it foreach (Node src : g) { if (r == src.representative) break; //skipping foreach (Node dst : src.getUnsampledNeighbors()) { /*pointer jumping operations as demostrated in Figure 1*/ } } |
Figure 2: Pseudocode for Pointer Jumping with subgraph sampling(7-9) algorithm.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | Graph g = /*input graph*/ do { updated = false; foreach (Node src : g) { if(src.old_label > src.curr_label){ src.old_label = src.curr_label; updated = true; foreach (Node dst : src.getNeighbors()){ atomicMin(dst.curr_label, src.curr_label); //atomicMin(A, B): atomic write B's value to A if A < B } } } } while(updated) |
Figure 3: Pseudocode for Label Propagation(10) algorithm.
Data Structures
There are two key data structures used in connected components:
- Graph
- An undirected graph.
- Union-Find
- A disjoint-set data structure used to maintain components of graph.
Performance
Figure 4 and Figure 5 show the execution time in seconds and self-relative speedup (speedup with respect to the single thread performance), respectively, of this algorithm running on a graph generated using rmat model with 225 nodes and 229 edges.
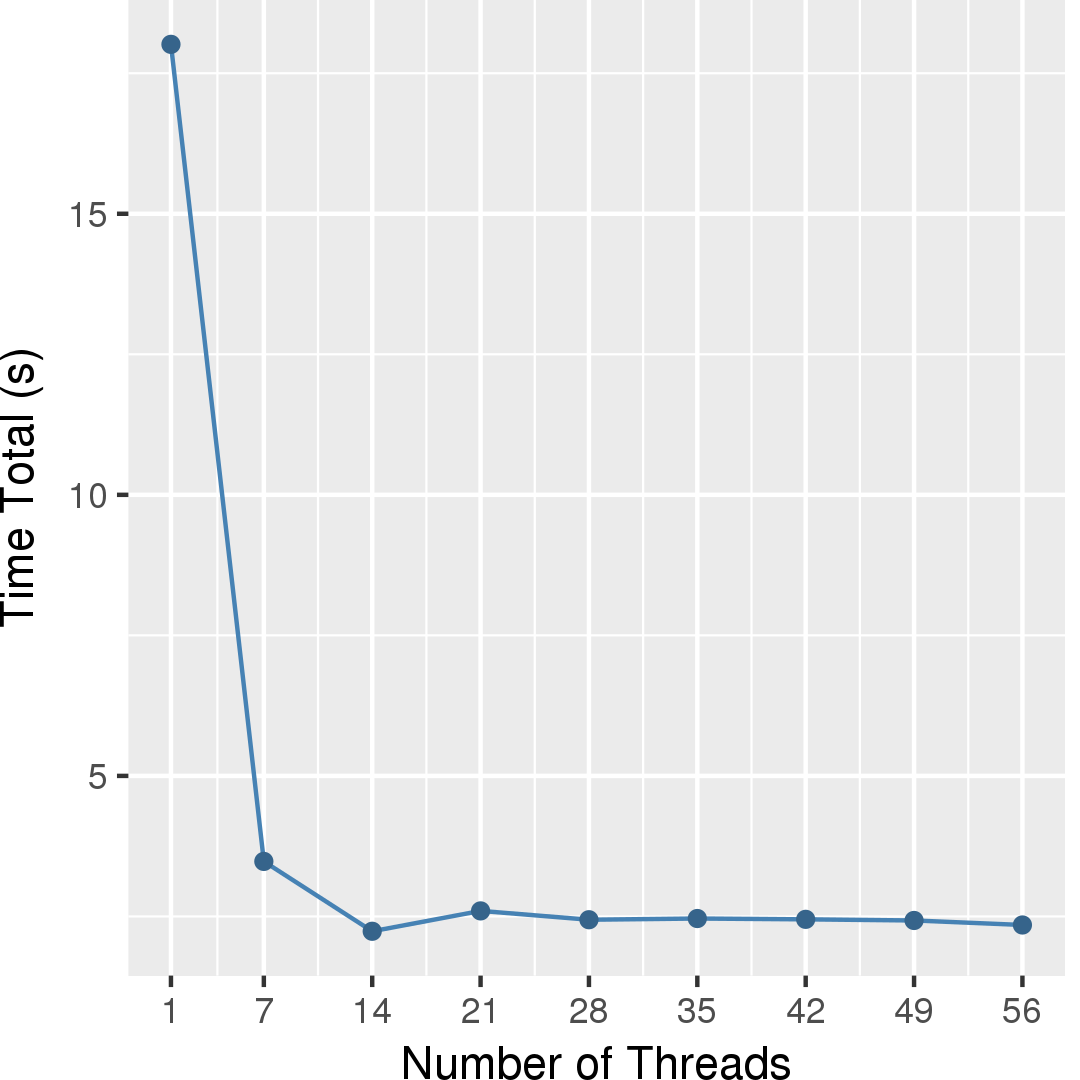
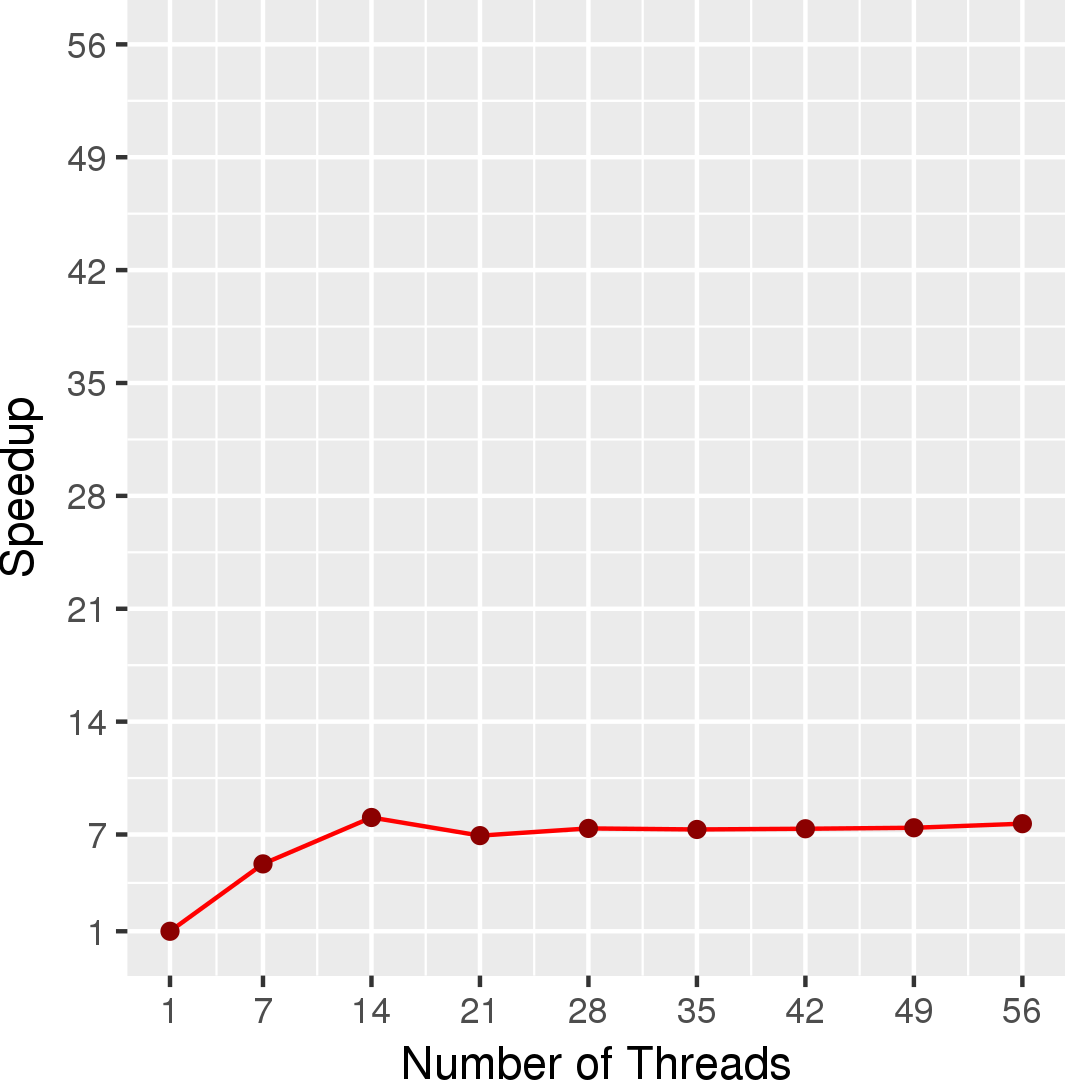
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
