Clustering
Application Description
This benchmark deals with extracting communities from large networks based on the louvain method, first proposed by Bondel et al. [1]. Finding an exact solution to this problem is known to be NP-Hard and the goal here is to compute a very good approximate solution efficiently.
Algorithm
This is a community-detection algorithm and is used to extract communities from large networks. This method was first proposed by Blondel et al. [1]. Each node is assigned to a community such that the resulting communities have large number of inter-community edges and small number of intra-community edges.
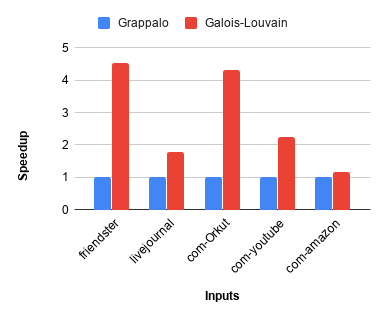
The state-of-the-art parallel implementation for this problem is due to the Grappalo framework [2]. Figure 1 describes the pseudocode of the Galois implementation of louvain clustering based on the parallel implementation in [2]. Here however we omit the coloring step in [2] and instead we use the galois::for_each to lock a node's neighborhood, while computing its new community assignment. Figure 2 illustrates how this modification speeds up the performance as compared to the implementation in [2].
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | Input: Graph g; Mod_curr <- 0; Mod_prev <- 0; while (Delta(Mod) > threshold){ while(true) { foreach (Node n: g) find the best community assignment for n that results in the highest modularity gain; Mod_curr <- calculate new modularity score; if(Mod_curr - Mod_prev < threshold) break; else Mod_prev <- Mod_curr; } g <- build new graph by merging nodes in the same community; } |
Figure 1: Pseudocode for Louvain Clustering
[1] Blondel, V.D., Guillaume, J.L., Lambiotte, R. and Lefebvre, E., 2008. Fast unfolding of communities in large networks. Journal of statistical mechanics: theory and experiment, 2008(10), p.P10008.
[2] Lu, H., Halappanavar, M. and Kalyanaraman, A., 2015. Parallel heuristics for scalable community detection. Parallel Computing, 47, pp.19-37.
Performance
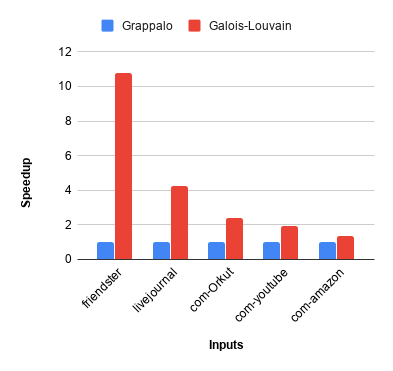
Figure 2 shows the relative speedup of non-deterministic Galois-Louvain compared to the Grappalo implementation with 8 threads. Figure 3 shows the relative speedup for the corresponding deterministic implementations.
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
