k-Core
Application Description
This benchmark finds the k-Core of a graph. The k-Core is defined as a subgraph G' in which all vertices have at least degree k in G'.
Algorithm
The k-Core decomposition algorithm prunes vertices of degree less than k from the
graph until no more vertices can be pruned.
Lonestar uses a worklist to compute k-Core in a data-driven manner.
First, the worklist is initialized with vertices that have degree less than k from
the input graph. Processing a vertex in the worklist involves decrementing the
degrees of its immediate neighbors by one. If a degree of the neighbor vertex falls
under the specified k, then it is added to the worklist. These steps are repeated
until there are no more vertices on the worklist.
| 1 2 3 4 5 6 | WorkList initialWL; for (Node n : graph) { if (n.currentDegree < specified_k) { initialWL.add(n); } } |
Figure 1: Initialize a worklist.
Lonestar's k-Core implementation has two types of algorithms that differ in how they maintain the worklist. The first is a Jacobi based algorithm called 'Sync'. In this method, the new worklist is constructed for each round and replaces the current worklist.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | WorkList current, next; initialWorkList(current); while (!current.empty()) { foreach (Node src : current) { foreach (Edge e : src.neighbors()) { Node dst = getEdgeDst(e); dst.currentDegree -= 1; if (dst.currentDegree < specified_k) { // Newly added vertices are not processed in this round. next.add(dst); } } } swap(current, next) } |
Figure 2: Synchronous k-Core algorithm
The second type is a Gauss-Seidel based algorithm called 'Async'. In this method, only one worklist is used, and vertices are pushed/popped to the worklist without any notion of rounds. This algorithm terminates when the worklist becomes empty.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | WorkList prunedNodes; initialWorkList(prunedNodes); // Terminate if the worklist is empty. foreach (Node src : prunedNodes) { foreach (Edge e : src.neighbors()) { Node dst = getEdgeDst(e); dst.currentDegree -= 1; if (dst.currentDegree < specified_k) { // Add to the worklist and // the added node is immediately visible for processing. prunedNodes.add(dst); } } } |
Figure 3: Asynchronous k-Core algorithm
Performance
Figure 4 and Figure 5 show the execution time in seconds and self-relative speedup of the synchronous k-Core algorithm (speedup with respect to the single thread performance), respectively, of this algorithm running on the Twitter graph.
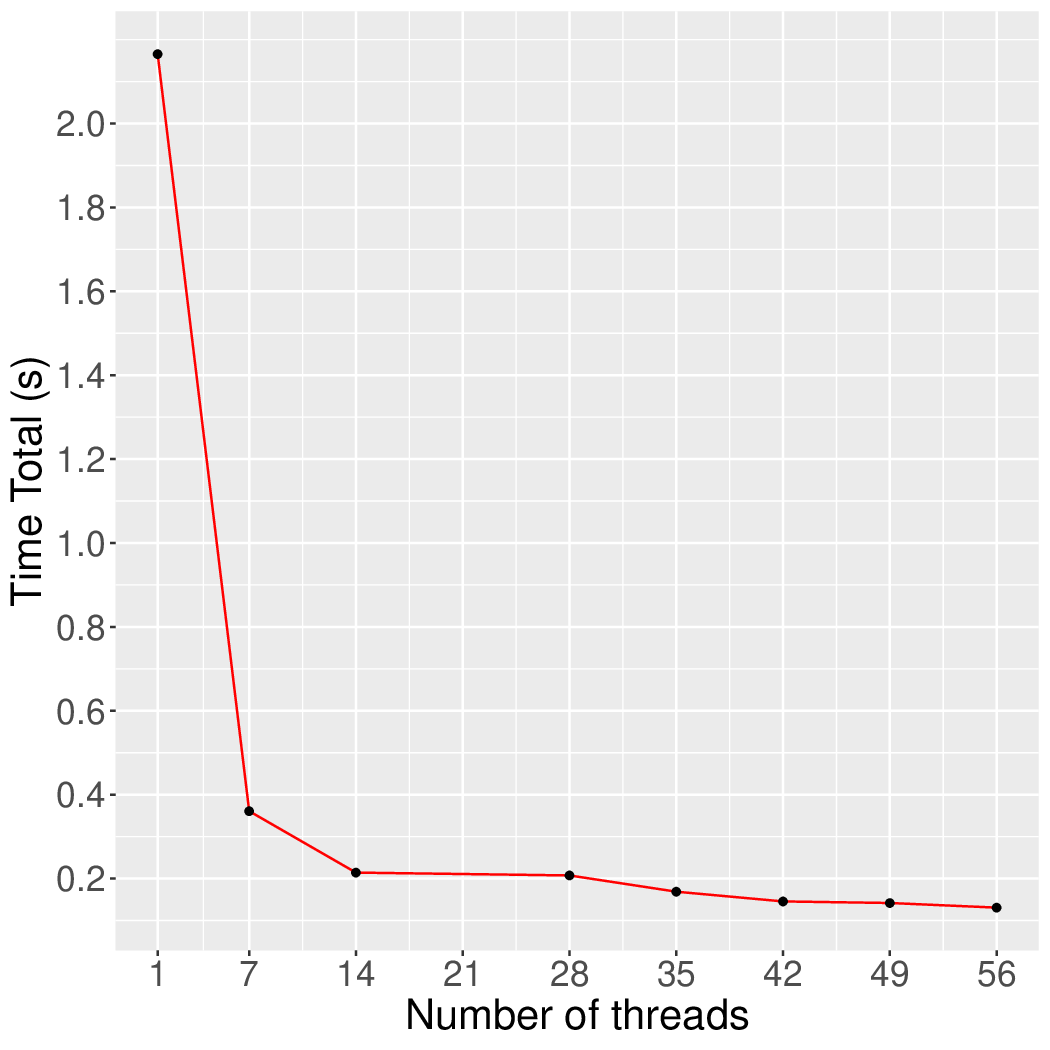
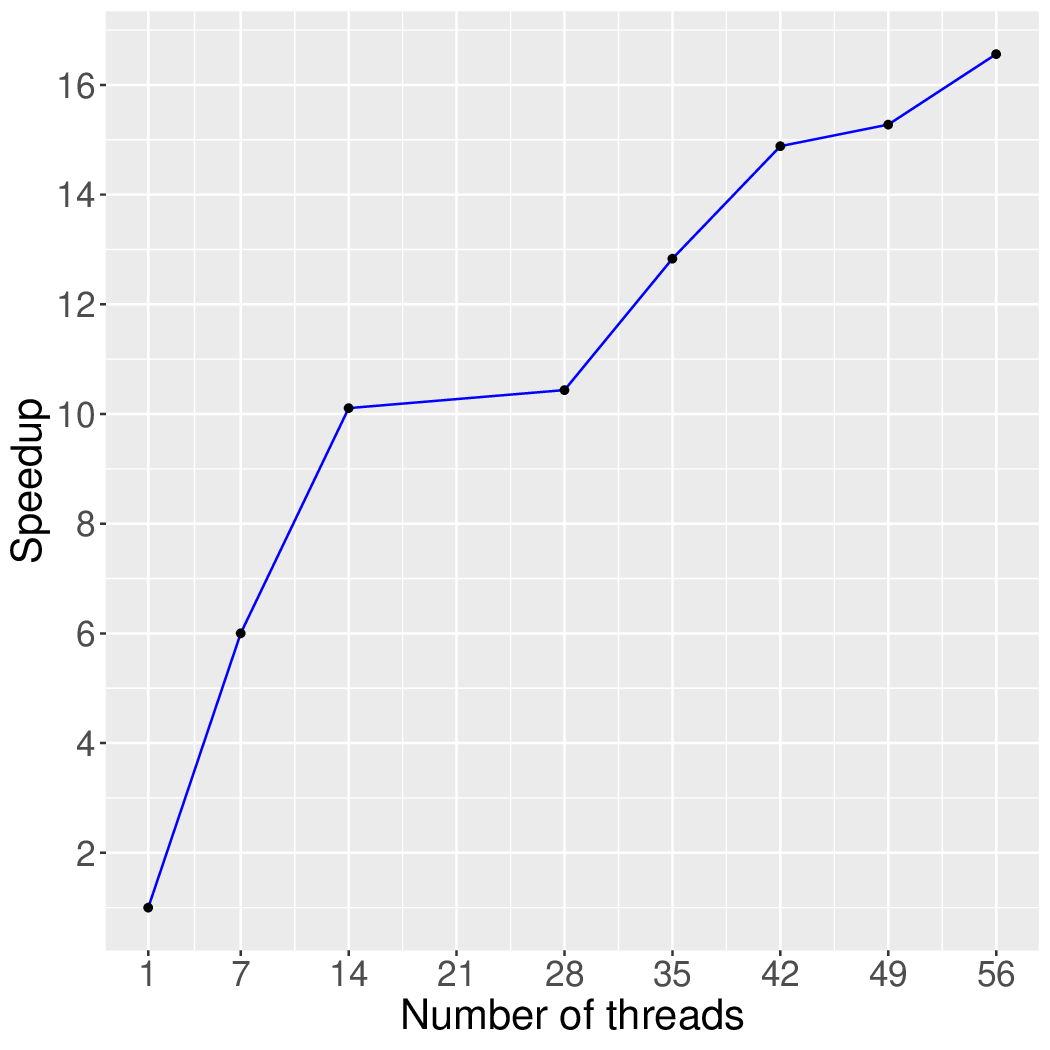
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
