Triangle Counting
Application Description
This benchmark counts the number of triangles in a given undirected graph. It implements the node-iterator and edge-iterator algorithms in [1], and it implements an ordered count algorithm (also used in the GAP benchmark suite). All nodes/edges can be processed independently.
[1] Thomas Schank. Algorithmic Aspects of Triangle-Based Network Analysis. PhD Thesis. Universitat Karlsruhe. 2007.
Algorithms
In the Node-iterator algorithm, for a pair of nodes a and b where both are node n's neighbors, if a is b's neighbor, and vice versa, then there is a triangle composed of nodes n, a, and b. Therefore, we can count triangles by scanning through all pairs of neighbors for all nodes and see if the pair of nodes are each other's neighbor. To avoid double counting, we count a triangle only if a < n < b by some criteria. This requires pre-sorting of edge lists for all nodes. Figure 1 shows the pseudocode for node-iterator algorithm.
| 1 2 3 4 5 6 7 8 9 10 11 12 | /* sort edge lists for all nodes */ num_triangles = 0; foreach (Node n: graph) { foreach (Node a: n's neighbor) { if (a >= n) continue; foreach (Node b: n's neighbor) { if (b > n and b is a's neighbor) { num_triangles++; } } } } |
Figure 1: Pseudocode for node iterator algorithm of triangle counting
In the Edge-iterator algorithm, given an edge e whose end points are n and m, if n and m have a common neighbor a, then there is a triangle formed by nodes n, m, and a. Hence, we can count triangles by intersecting each edge's end points' edge lists and summing all intersections' sizes. To avoid double counting, we only consider n < a < m by some criteria when intersecting edge lists. This requires pre-sorting of edge lists for all nodes. Figure 2 shows the pseudocode for edge-iterator algorithm.
| 1 2 3 4 5 6 7 8 9 | /* sort edge lists for all nodes */ num_triangles = 0; foreach (Edge e: graph) { Node n = e.src; Node m = e.dst; NodeSet n_ngh = {s| s is n's neighbor and n < s < m}; NodeSet m_ngh = {t| t is m's neighbor and n < t < m}; num_triangles += |n_ngh intersect m_mgh|; } |
Figure 2: Pseudocode for edge-iterator algorithm of triangle counting
The ordered count algorithm relies on a sorted vertex order of the graph in which high-degree nodes appear first. It then functions similarly to the node-iterator algorithm: threads handle nodes separately, and a triangle a, b, c is only counted if a > b > c. Since high-degree nodes appear at the beginning, they will count no triangles, reducing the number of iterations of the outer-most loop and overall computation time. For example, the thread with a = 0 (the highest-degree node in the graph) will do no work as all vertices have an ID greater than 0: a will never be greater than any other b. This algorithm works well if the degree distribution is uneven (e.g., power-law graphs where only a few nodes have very high degree).
Parallelism
All of our algorithm implementations are topology-driven algorithms, since all nodes/edges are active. The graph is only read, so all activities at nodes/edges can proceed independently.
Performance
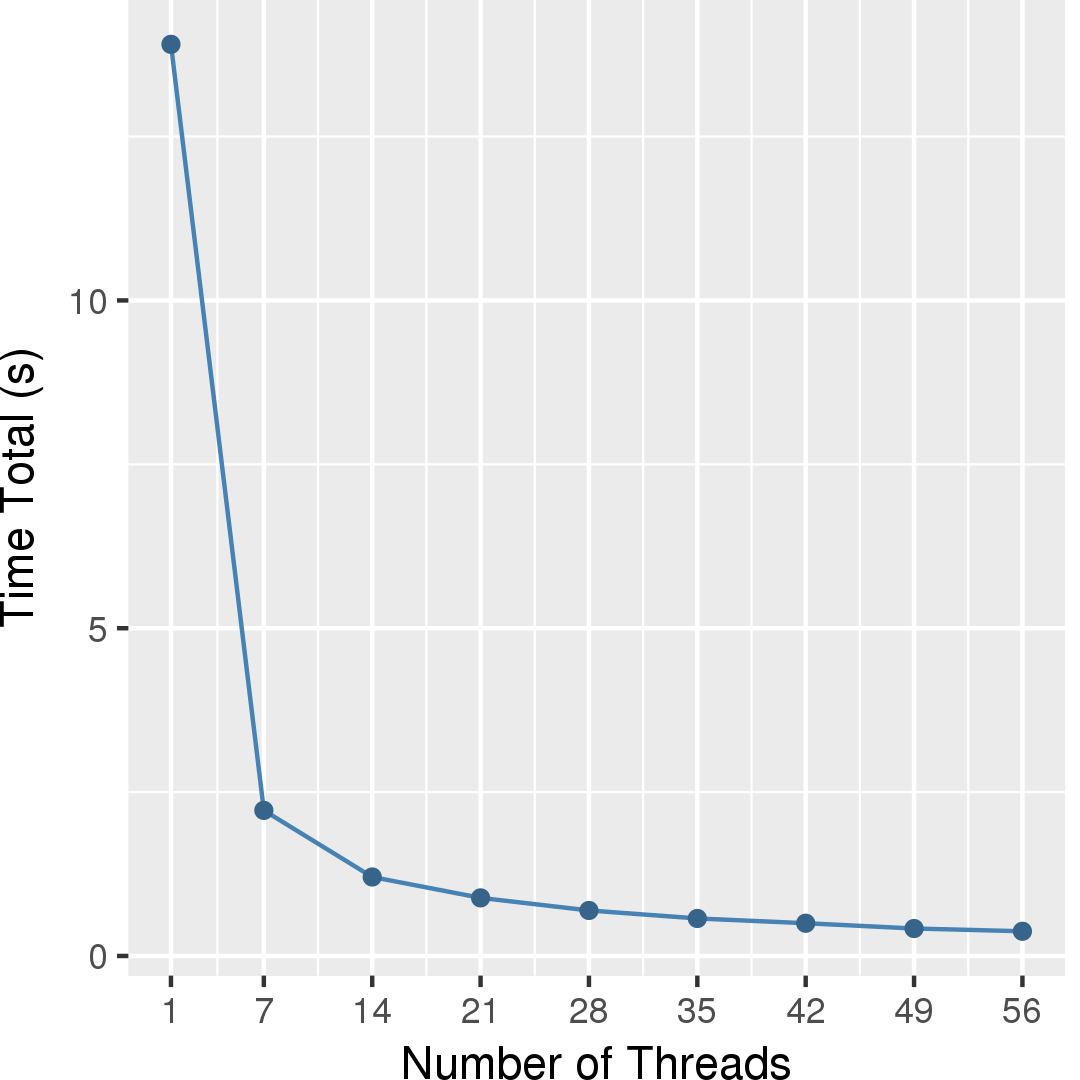
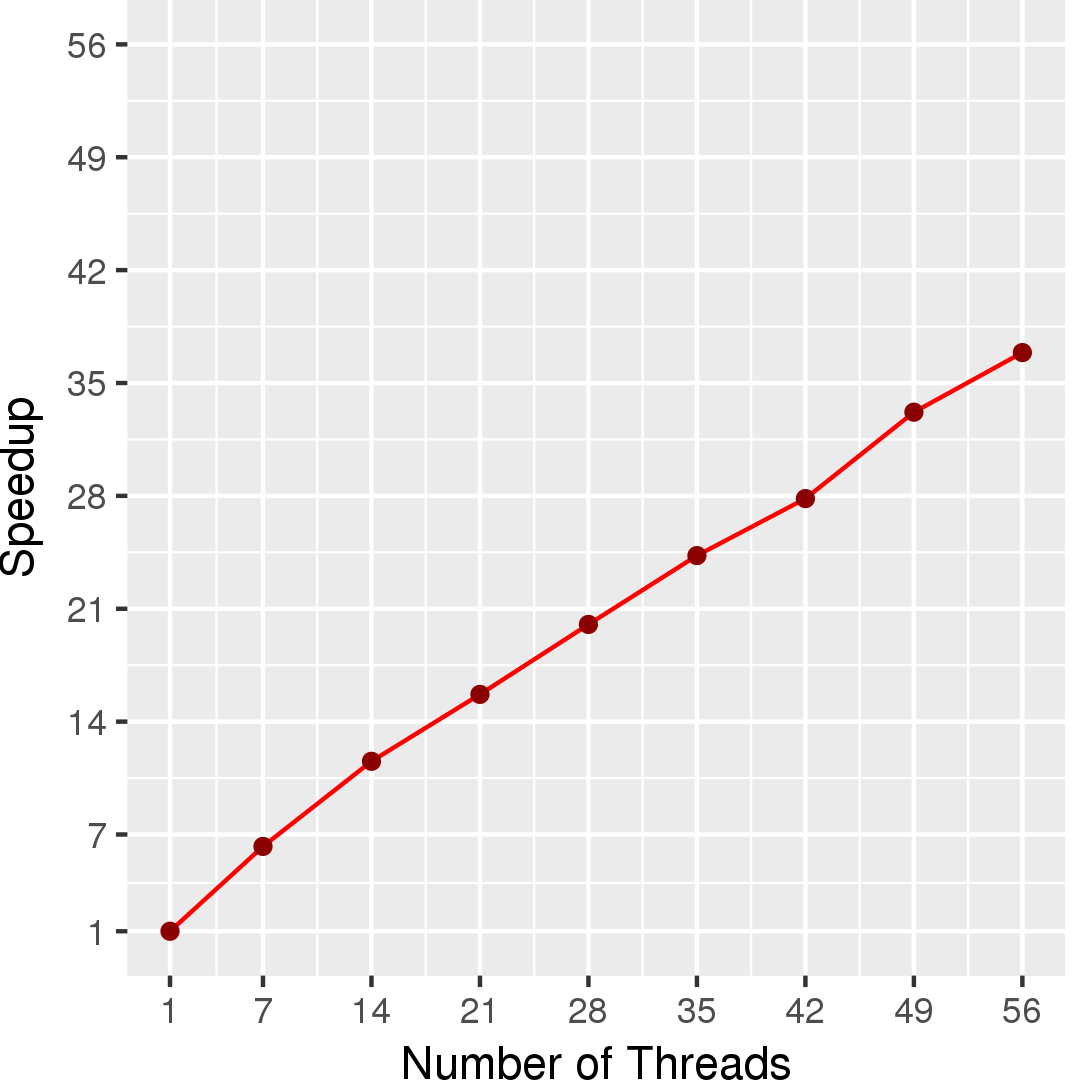
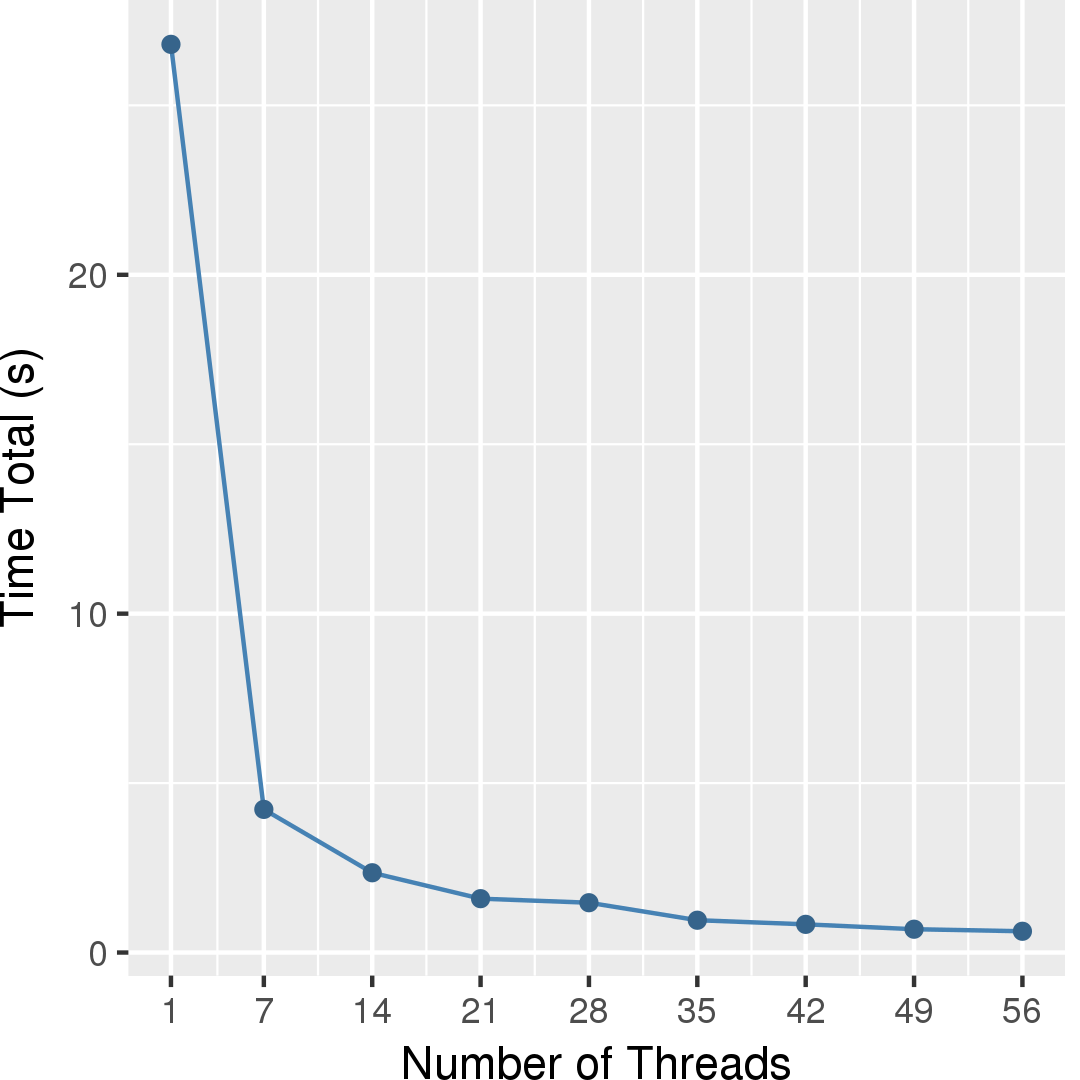
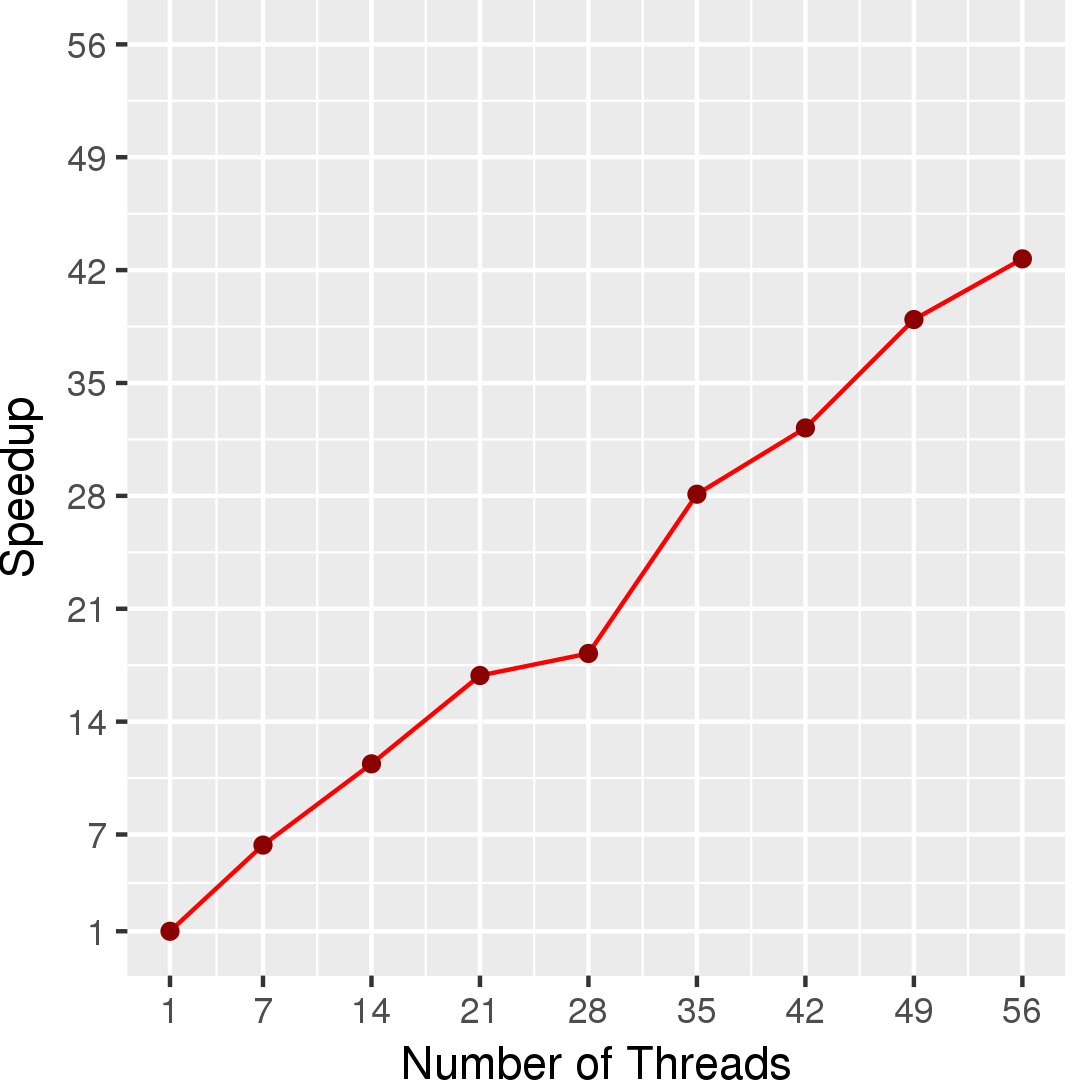
Figures 2, 4, and 6 show the execution time of the edge-iterator algorithm, the node-iterator algorithm, and the ordered count algorithm, respectively. Figures 3, 5, and 7 show the self-relative speedup, i.e, speedup with respect to the single thread performance for edge-iterator, node-iterator, and ordered count algorithm, respectively. The input is LiveJournal graph, and the number of triangles present in the graph is 285730264.
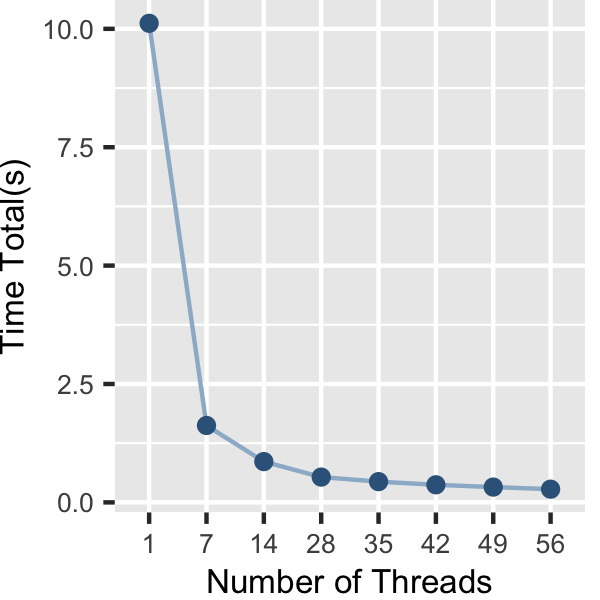
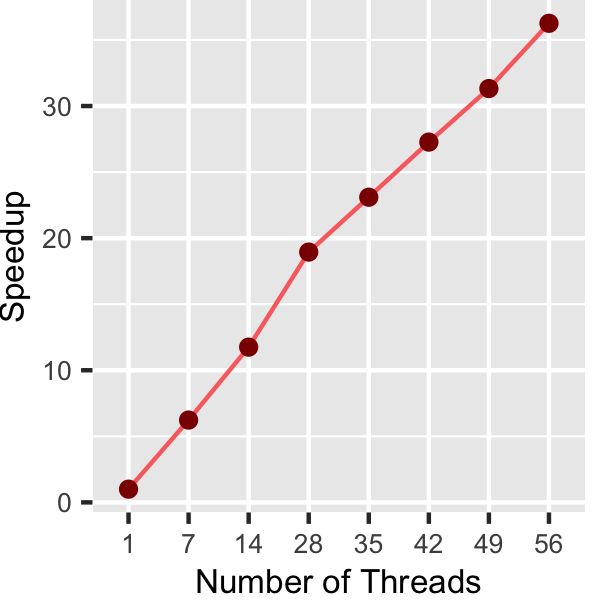
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
