Delaunay Triangulation
Application Description
This benchmark produces a Delaunay triangulation from a given a set of points. It implements the algorithm proposed by Bowyer [1] and Watson [2]. The amorphous data parallelism in this algorithm arises from the worklist of triangles containing points that must be inserted into the mesh.
[1] Adrian Bowyer. Computing Dirichlet tessellations, The Computer Journal, Vol. 24, No. 2, pp 162 - 166, 1981.
[2] David F. Watson. Computing the n-dimensional tessellation with application to Voronoi polytopes, The Computer Journal, Vol. 24, No. 2, pp 167 - 172, 1981.
Algorithm
A 2D Delaunay mesh is a triangulation of a set of points with the following property: the circumcircle of any triangle in the mesh must contain no other point from the mesh. The algorithm takes as input a set of 2D points contained inside a surrounding triangle. It iteratively builds the Delaunay mesh by inserting a new point and re-triangulating the affected portions of the mesh. The output is a Delaunay triangulation in which the set of vertices is equal to the set of input points.
One implementation is as follows. There is a list of points to be inserted in the mesh. There is a quad-tree that contains points already added to the mesh and which facilitates finding the nearest point in the mesh for each point to be added. Each point in the mesh has a link to an arbitrarily chosen triangle that is incident on it. Initially, the mesh in a single large triangle that covers all the points to be added.
In each step, the triangulation procedure, (1) picks a point p from a worklist, (2) finds the closest point q in the mesh to p, (3) from the triangle associated with q, searches for the triangle in the mesh, t, that contains p, (4) collects the triangles in the mesh centered around t whose circumcircle contains p (i.e., the cavity of p), and (5) re-triangulates the cavity. The order in which the triangles are processed is irrelevant, and all orders lead to the same valid Delaunay mesh, so this is an unordered algorithm. Periodically, the quad-tree is updated with all the new points added to the mesh.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | Set<Point> points = /* read points to insert */; Mesh m = new Mesh(); Triangle large = new Triangle(points); m.add(large); Workset ws = new Workset(); ws.addAll(points); QuadTree tree = new QuadTree(); foreach (Point p : ws) { Point q = tree.find(p) Triangle t = findContainingTriangle(p, q); Cavity c = new Cavity(t, p); c.expand(); c.retrianglate(); m.updateMesh(c); if (*) tree.update(...) } |
Figure 1: Pseudocode for Delaunay triangulation.
Data Structures
There are three key data structures used in Delaunay triangulation:
- Unordered Set
- The worklist used to hold the triangles is represented as an unordered set.
- Graph
- The mesh is represented as a graph. The triangles in the mesh are represented as nodes in the graph, and triangle adjacency is expressed through edges between nodes.
- Quad tree
- A quad tree is used to easily find points in the mesh near the point to be added. It does not need to be exact. It is periodically regenerated.
Parallelism
The active elements in Delaunay triangulation are the points to be inserted into the mesh, and they can be processed in any order. Inserting a point requires building a cavity; the affected triangles are in the processed triangle's neighborhood. Because these neighborhoods are typically small connected regions of the mesh, significant parallelism can be achieved by inserting multiple points in parallel, provided the cavities are far enough apart in the mesh. Conflicts between concurrently executing insertions occur when neighborhoods overlap.
Figure 2 shows the available parallelism of Delaunay triangulation, for a random input consisting of 1,000,000 points. Delaunay Triangulation is a graph refinement code. Point insertion removes a subgraph from the graph (representing the cavity of the inserted point) and replaces it with a larger subgraph (the updated cavity). At the beginning of the computation, there is effectively no parallelism because the initial mesh is very small, consisting of a single triangle. Then, the available parallelism increases as the size of the graph increases until the algorithm starts running out of work.
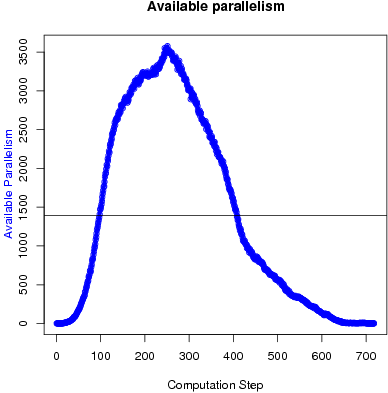
Figure 2: Available parallelism in Delaunay triangulation.
Performance
Figure 3 and Figure 4 show the total running time and self-relative speedup (speedup with respect to the single thread performance), respectively, of the code for an input comprising of about 5 million points. On the same input, Triangle program takes about 236 seconds.
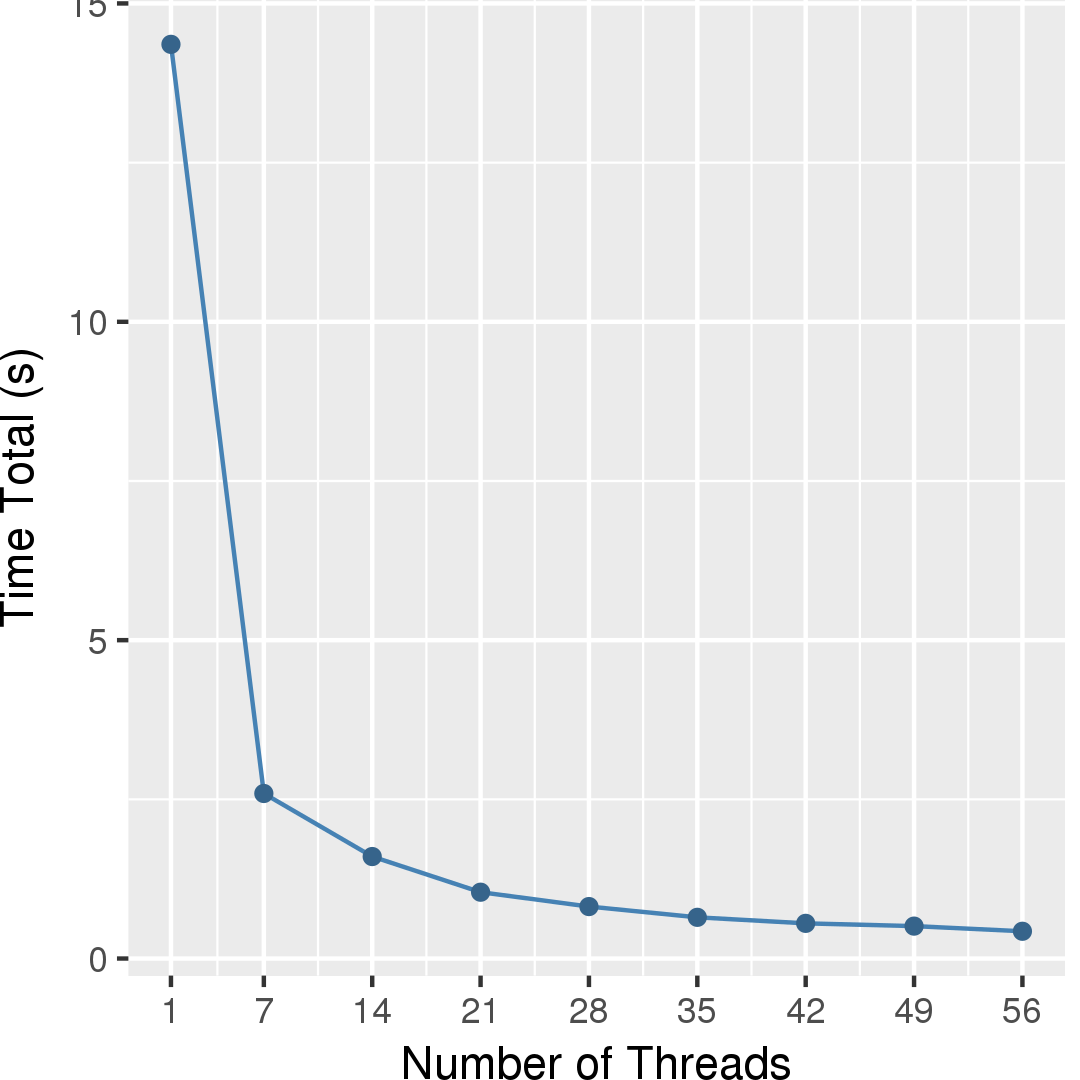
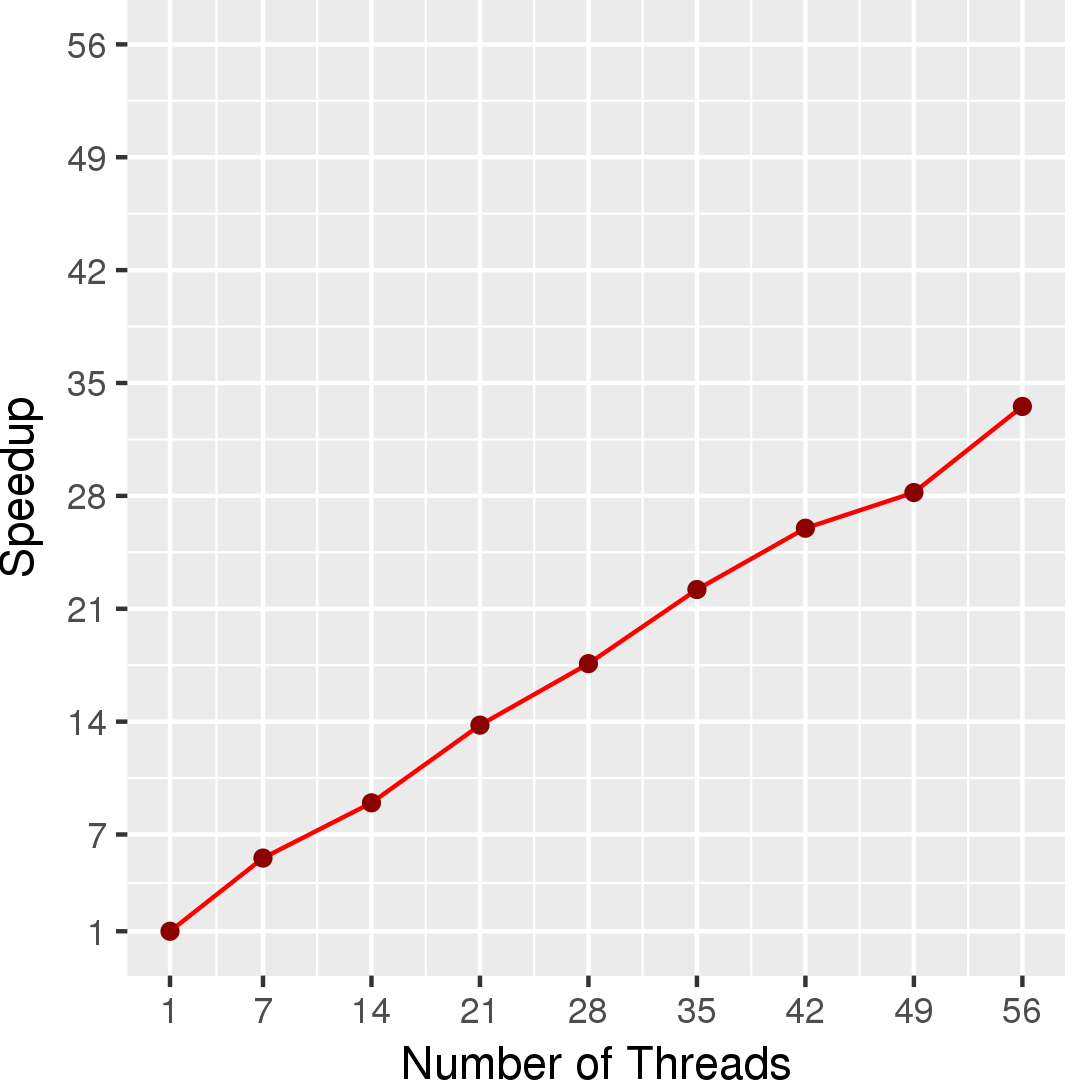
The scalability is limited due to the time it takes to generate the quad tree, which is currently done in serial.
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
