AIG Rewriting
Application Description
In logic synthesis, a combinational circuit C can be represented as an And-Inverter graph (AIG). This benchmark optimizes a given circuit C by reducing the number of nodes in G, the AIG for C, while keeping C's functionality the same. The reduction is done by replacing sub-graphs of G with their functionally equivalent ones that have fewer nodes.
Algorithm
DAG-aware AIG rewriting works as follows. Nodes are processed in topological order. When processing a node n, feasible k-cuts rooted at n are enumerated, and the current k-cut is replaced with a feasible k-cut that has the least number of nodes.
Figure 1 shows the pseudocode for AIG rewriting. Line 1 reads in the AIG graph. Line 2 populates the work set with primary inputs. Line 4 enumerates feasible k-cuts rooted at an active node. Line 5-9 pick a feasible k-cut that reduces the number of nodes the most. Line 10-11 perform the replacement. Finally, Line 12-16 ensure that nodes are activated in topological order.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | AIG g = /* read AIG */; Workset ws = new WorkSet(g.getPrimaryInputs()); foreach (Node n: ws) { CutSet cs = /* the set of feasible k-cuts rooted at n */; KCut cur_cut = /* current k-cut rooted at n */; KCut best_cut = cur_cut; for (KCut c: cs) if (|best_cut| > |c|) best_cut = c; if (best_cut != cur_cut) g.replace(cur_cut, best_cut); for (Node succ: g.edges(n)) { succ.dep--; if (succ.dep == 0) ws.add(succ); } } |
Figure 1: Pseudocode for AIG rewriting
For more details, please refer to [1].
[1] Vinicius Possani, Yi-Shan Lu, Alan Mishchenko, Keshav Pingali, Renato Ribas, André Reis. Unlocking Fine-Grain Parallelism for AIG Rewriting. In ICCAD 2018.
Data Structures
The input AIG the data structure used in AIG rewriting.
Parallelism
AIG rewriting is a data-driven algorithm, since a node can be rewritten only after all its predecessors have been rewritten. The parallelism exists among active nodes whose unions of feasible k-cuts do not overlap.
Performance
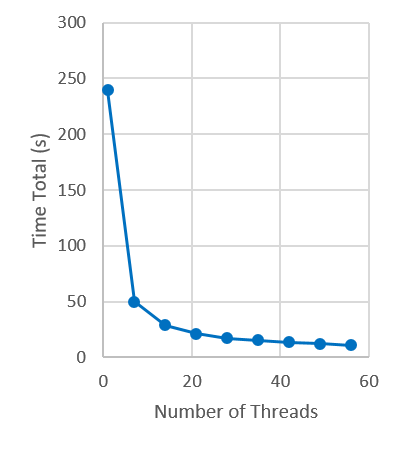
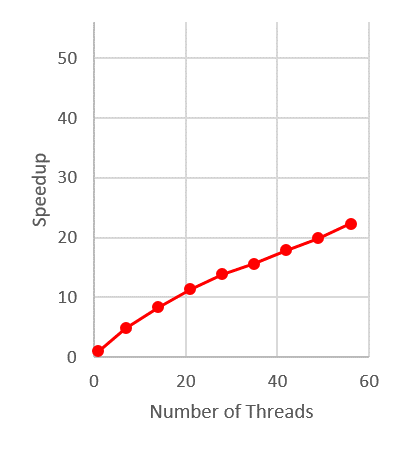
Figure 2 shows the execution time. Figure 3 shows the self-relative speedup, i.e, speedup with respect to the single thread performance. The input is mem_ctrl doubled 10 times by abc.
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
