Matrix Completion
Application Description
Matrix completion is an application which fills the missing entries in a partially observed or filled matrix. One example is the movie-ratings matrix in the Netflix Problem: Given a rating matrix in which entry (i,j) represents the rating given to movie i by user j if user has watched that movie,
otherwise that entry will be missing in the matrix. Now the problem is to predict the values of the missing entires as accurately as possible in order to make good recommendations to the users to watch new movies.
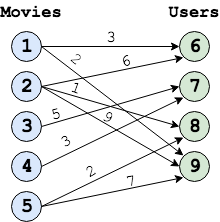
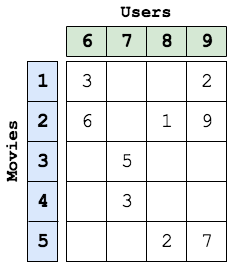
The input to matrix completion is a bipartite graph. Figure 1 shows an example of a movie rating bipartite graph. Figure 2 shows the equivalent matix representation of the bipartite graph in Figure 1.The edges of the bipartite graph represent the filled entries in the matrix form of the graph and the edge values from node i to node j represents the rating given to movie i by user j. The numbers on the movie and user nodes represent the node IDs for the nodes of the graph as expected by this application is Galois. All the movie nodes (or nodes with out-going edges) must be laid out first with IDs 0 to N, followed by user nodes form N+1 to M, assuming that total number of movie nodes is N and total number of user nodes is M. In Figure 1, N is 5 and M is 4.
Algorithms
To solve matrix completion, Galois provides 2 algorithms, Stochastic Gradient Descent (SGD) and Alternating Least Squares (ALS) as discussed below:
Stochastic Gradient Descent (SGD)
SGD is an iterative method for optimizing a differentiable objective function, a stochastic approximation of gradient descent optimization. In matrix completion, node label (movie as well as user node labels) is associated with an array of fixed size, known as Latent Array or Feature Array . The size of feature array can be varied: larger size gives more accurate predictions but also requires more compute.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | foreach (MovieNode n: graph) { movie_LA = n.latent_array foreach (UserNode m: n's neighbor) { user_LA = m.latent_array new_rating = dotProduct(movie_LA, user_LA) error = edge_value - new_rating for(i: LATENT_ARRAY_SIZE) { prevMovie = movie_LA[i] prevUser = user_LA[i] movie_LA[i] -= stepsize * ( error * prevUser + lambda * prevMovie) user_LA[i] -= stepsize * ( error * prevMovie + lambda * prevUser) } } } |
Figure 3: Pseudocode for SGD algorithm of matrix completion
By iteratively updating the latent arrays of movies and users, SGD tries to minimize the root mean square error (RMSE), where error refers to the difference in the observed edge values and new edge values calculated from the latent arrays. SGD terminates after the RMSE falls below a certain threshold, which is a parameter to the application.
Parallelism
From Figure 3, we can see that SGD updates both the movie (source) and user (destination) latent arrays of node labels, therefore, edges with overlapping movies (sources) or users (destinations) can not be computed in parallel. In order to exploit parallelism, Galois provides 4 different schedules:
- sgdByItems : This is a very basic scheduling policy, in which movies (or items) are distributed among threads and each thread is responsible for all the out-going edges of the movies assigned to it, which can lead to load imbalance. Before updating an edge, each thread takes lock on the movie (source) and user (destination). There will be no conflicts on the movies (sources) since each movie is uniquely assigned to a thread, but different movies may have edges to the same user (destination), hence locks on users are required.
- sgdByEdges : In this scheduling policy, edges are distributed among threads to improve load balance. Lock is required on the user nodes before updating in this policy as well.
- sgdBlockEdge : This policy uses Fixed 2D Graph Tiled Executor provided by Galois, which divides the movie and user nodes in to 2D blocks. Each thread works on a given block of movies and users. Now lock is required at the granularity of a block rather than node. This also balances work well among threads, but can reduce the amount of parallelism if lots of users are shared among blocks. The number of movies and users in a block can be controlled by a commandline argument.
- sgdBlockJump : This policy also blocks the movies and users into 2D blocks and requires locking at the granularity of the blocks, but improves over sgdBlockEdge by dynamically assigning free blocks that require work to threads rather than waiting for locks to be released. The number of movies and users in a block can be controlled by a commandline argument.
Performance
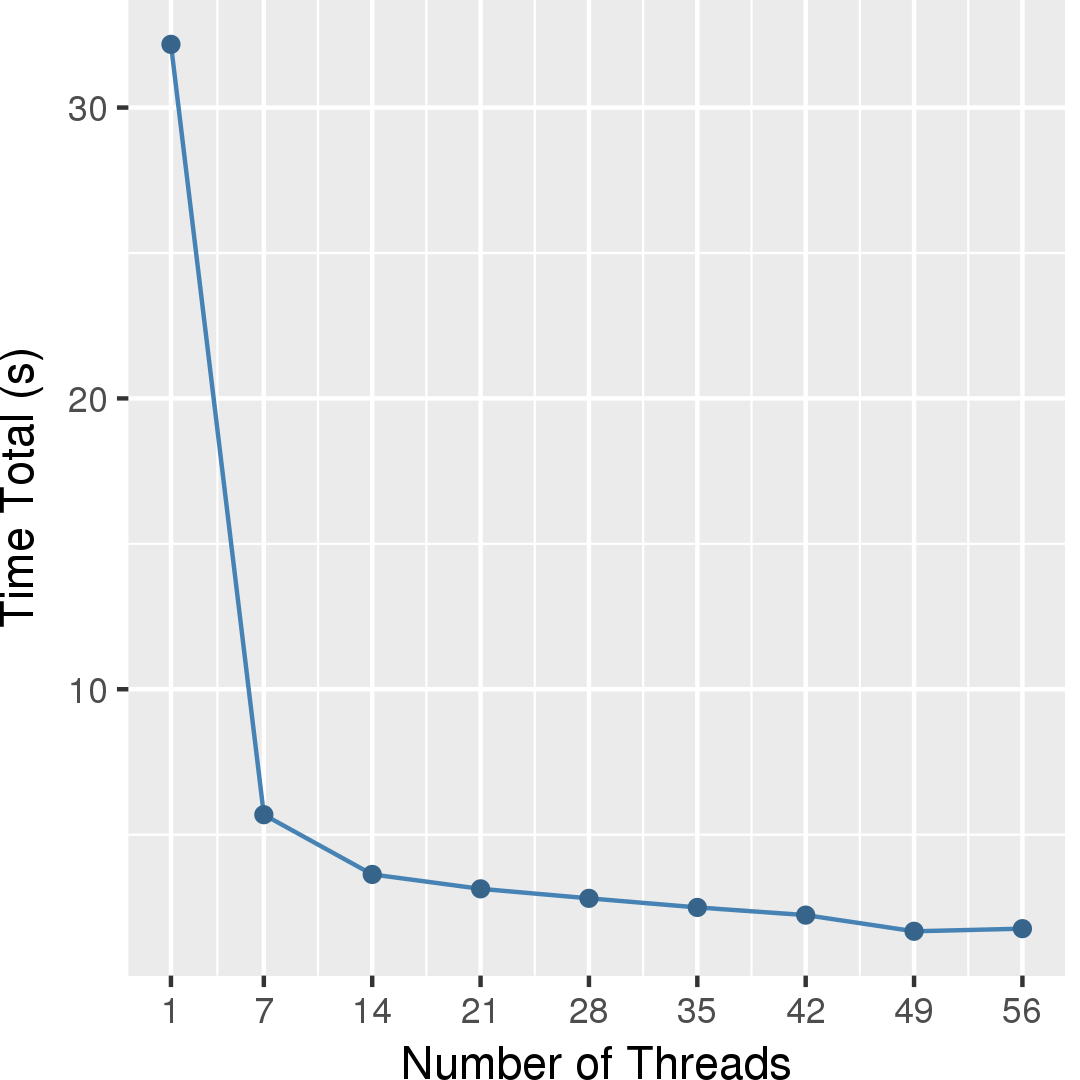
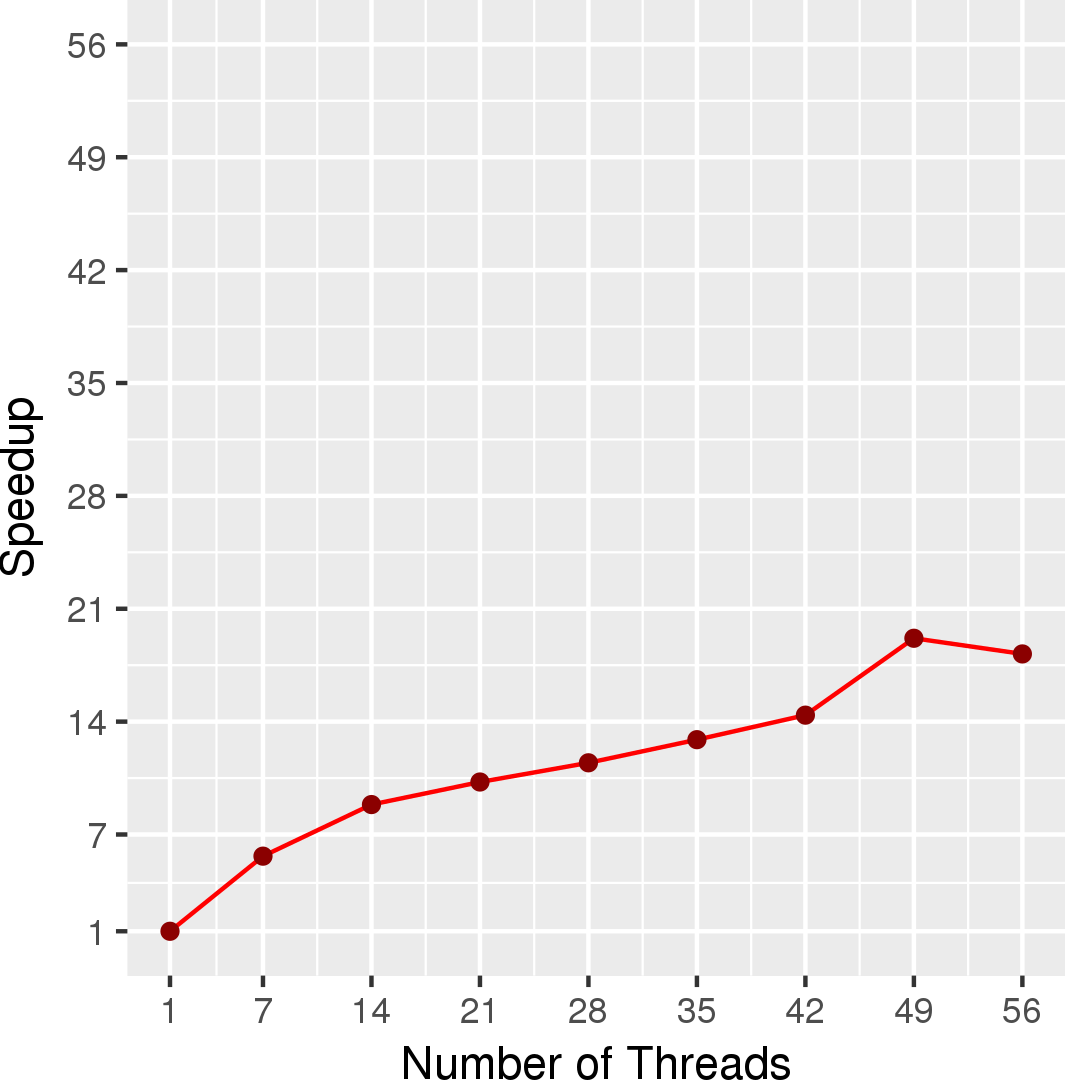
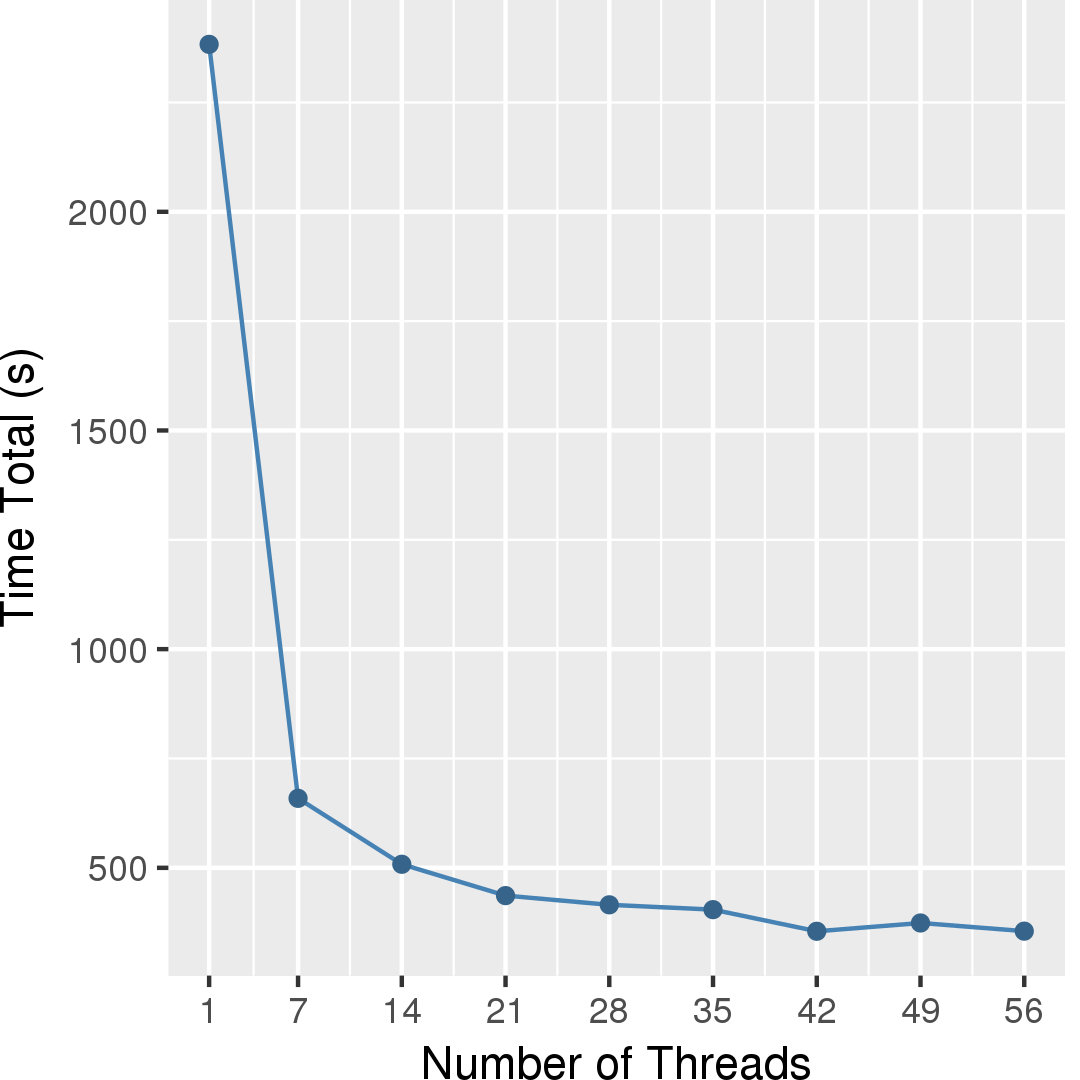
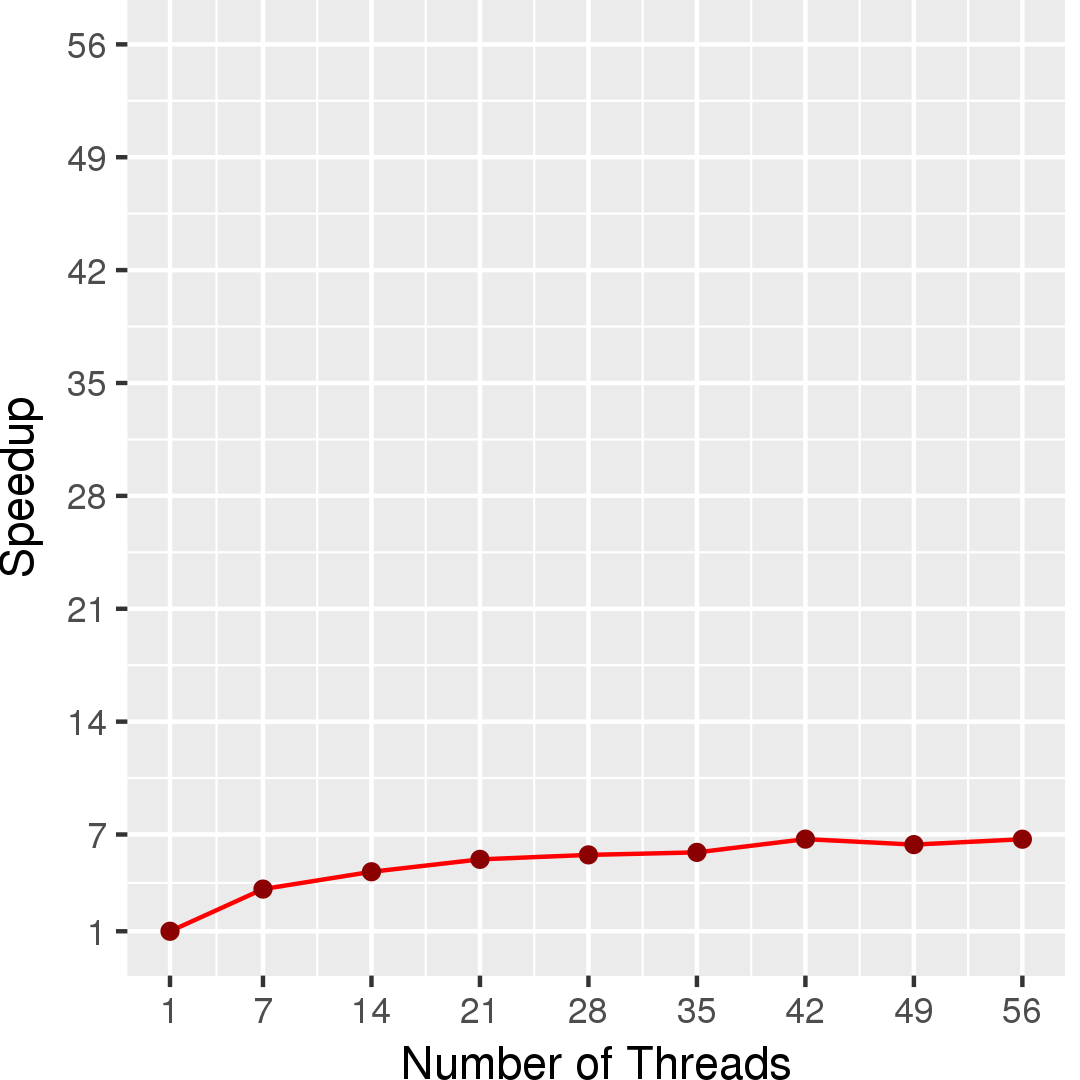
Figures 4 and 5 show the execution time and the self-relative speedup, i.e, speedup with respect to the single thread performance for sgdBlockEdge algorithm, respectively. The input is Netflix graph.
Alternating Least Squares (ALS)
Alternating Least Squares (ALS) represents a different approach to optimizing the objective (loss) function. This application also provides 2 ALS algorithms for matrix completion.
- simpleALS
- syncALS
Performance
Figures 6 and 7 show the execution time and the self-relative speedup, i.e, speedup with respect to the single thread performance for simpleALS algorithm, respectively. The input is Netflix graph.
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
