k-Truss
Application Description
This benchmark finds the k-Truss of a graph. The k-Truss is defined as a maximal connected subgraph G' in which all edges are part of at least (k-2) triangles in G'.
Algorithm
The k-Truss algorithm prunes edges which are not included in at least (k-2) triangles until no more edges are required to be pruned. The Lonestar benchmark suite has three variants of the k-Truss: bsp-jacobi, bsp, and core-then-truss. All the k-Truss variants first mark all the edges 'valid.' The bsp-jacobi algorithm is a round-based algorithm, i.e., bulk-synchronous parallel (BSP). In round R, each edge computes its support (the number of triangles it will be part of). An edge is removed in round R+1 if its support is less than k-2 in round R. Execution continues until no more edges can be removed. Edge removals are done Jacobi-style: removed edges detected in round R will only be seen as removed from round R+1.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | currValidEdges = allEdges while (true) { removedEdges = empty; nextValidEdges = empty; for (Edge e : currValidEdges) { if (e is included in less than (k-2) triangles) { removedEdges.add(e); } else { nextValidEdges.add(e); } } if (removedEdges.empty()) { break; } for (Edge e : removedEdges) { mark e as 'invalid'; } currValidEdges = nextValidEdges; } return currValidEdges; |
Figure 1: Bulk-synchronous parallel-jacobi k-Truss.
The bsp algorithm behaves the same as the bsp-jacobi algorithm except that edge removals in round R are immediately visible in round R. This enables bsp to use fewer rounds to converge compared to bsp-jacobi since removed edges are visible earlier which can result in more edge removals in the same round. In other words, edge removal in the bsp algorithm is Gauss-Seidel-style.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | currValidEdges = allEdges; while (true) { nextValidEdges = empty; for (Edge e : currValidEdges) { if (e is invalid) { continue; } if (e is included in less than (k-2) triangles) { mark e as 'invalid'; } else { nextValidEdges.add(e); } } if (nextValidEdges.size() == currValidEdges().size()) { break; } currValidEdges = nextValidEdges; } return currValidEdges; |
Figure 2: Bulk-synchronous parallel k-Truss.
The core-then-truss algorithm is based on the observation that a k-Truss is always a (k-1)-Core, a maximal connected subgraph in which every node has at least k-1 neighbors. It computes (k-1)-Core, eliminating nodes with degree less than (k-1) and their connected edges, and then starts the k-Truss computation on the (k-1)-Core. Therefore, the core-then-truss algorithm requires less number of edge reads compared to the other two algorithms. We use the bsp k-Core algorithm to find the (k-1)-Core from a given graph and to find the k-Truss from the (k-1)-Core.
| 1 2 3 4 | if (k - 2 == 0) { return ; } bspCore(g, k-1); bspTruss(g, k); |
Figure 3: (k-1)-Core then k-Truss algorithm.
Performance
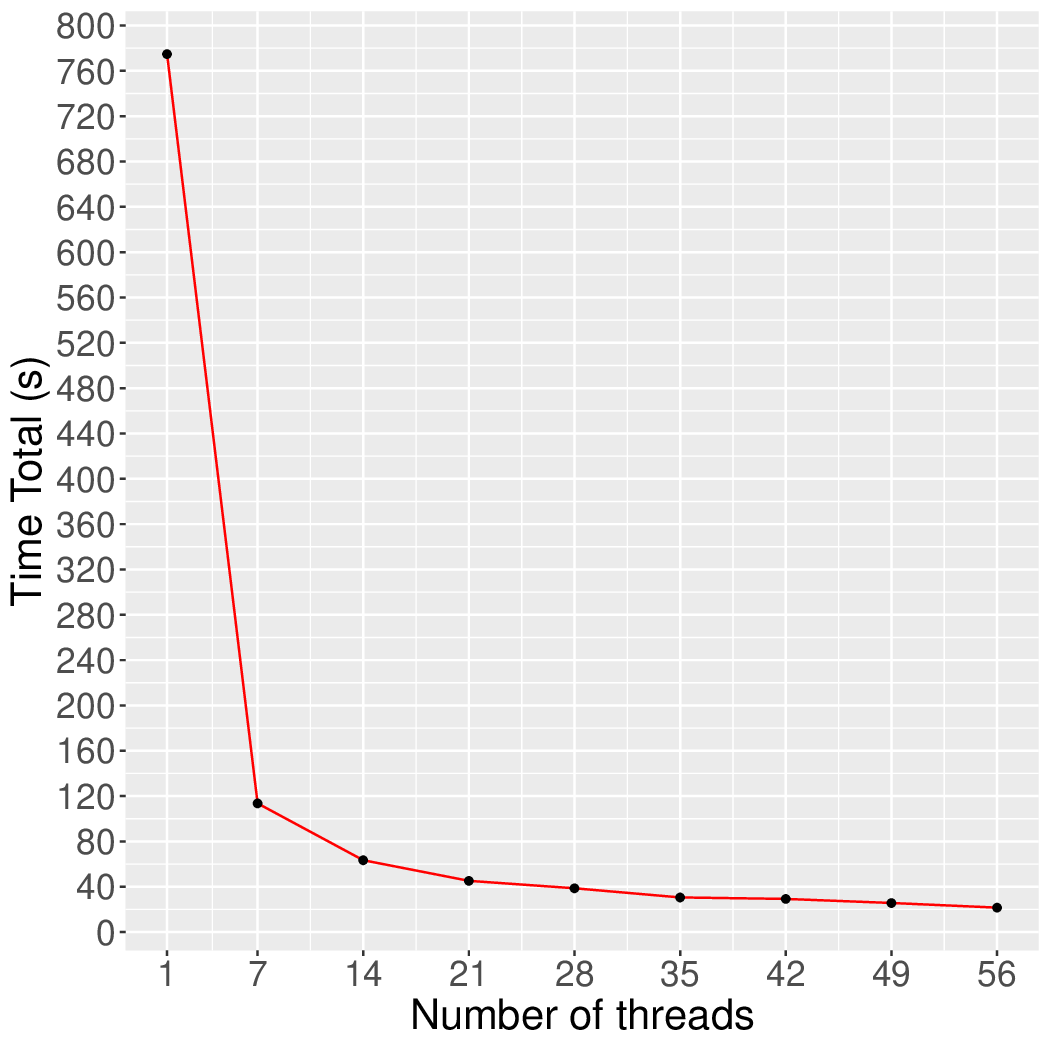
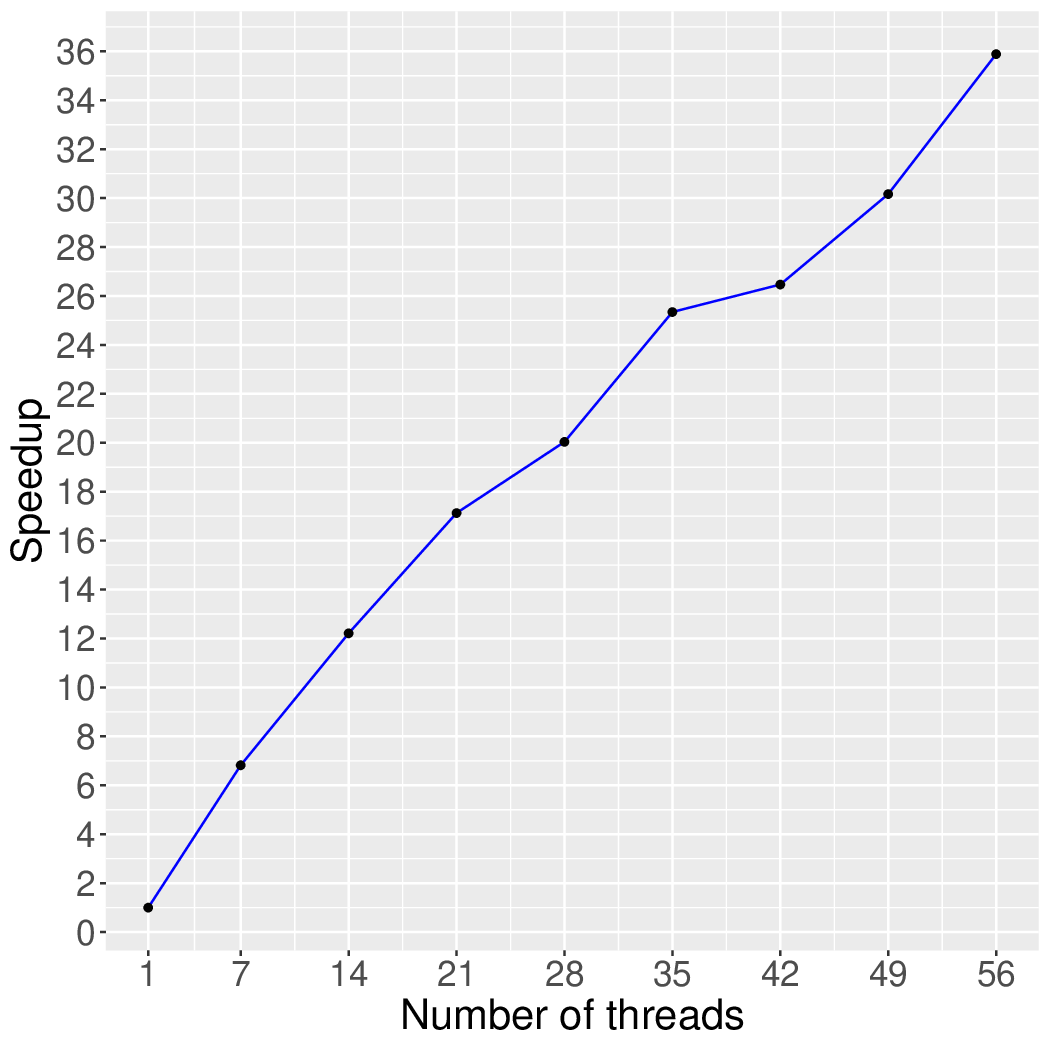
Figure 4 and Figure 5 show the execution time in seconds and self-relative speedup of the synchronous k-Truss algorithm (speedup with respect to the single thread performance), respectively, of this algorithm running on the eukarya protein graph.
Machine Description
Performance numbers are collected on a 4 package (14 cores per package) Intel(R) Xeon(R) Gold 5120 CPU machine at 2.20GHz from 1 thread to 56 threads in increments of 7 threads. The machine has 192GB of RAM. The operating system is CentOS Linux release 7.5.1804. All runs of the Galois benchmarks used gcc/g++ 7.2 to compile.
