k-Core
Problem Description
k-Core Decomposition is an application on undirected graphs that finds the k-Core in a graph. A k-Core is defined as a subgraph of a graph in which all vertices of degree less than k have been removed from the graph. The remaining nodes must all have a degree of at least k. This calculation is accomplished by incrementally removing nodes with degree less than k (which in turn lowers the degree of remaining nodes) until no more nodes are removed.
Link To Related Wikipedia PageAlgorithm
Our k-Core supports both execution models: bulk-synchronous parallel (BSP) and bulk-asynchronous parallel (BASP). For the computation phase in both the execution models, we remove nodes with a degree less than k from consideration when counting degrees for other graphs. This process is repeated until no node is removed. For BSP execution model, the execution occurs in rounds: computation followed by a bulk synchronous communication. In BASP execution model, the notion of rounds is eliminated, and a host performs computation at its own pace while an underlying messaging system ingests messages from remote hosts and incorporates boundary node label updates into the local partition of the graph.
We have two variants for computation phase: push and pull. In the push variant, when a node is removed from the graph, it decrements the degree of its neighbors. In the pull variant, a node checks its neighbors to see if any node has been removed in the previous round and decrements its degree for every newly decremented node. Pseudocode follows:
| 1 2 3 4 5 6 7 8 9 | for (node n in graph) { if (n alive last round) { if (n is marked removed) { for (neighbor a of node n) { a.degree-- } } } } |
Figure 1: Pseudocode for k-Core Push computation
| 1 2 3 4 5 6 7 8 9 | for (node n in graph) { for (neighbor a of node n) { if (a alive last round) { if (a is marked removed) { n.degree-- } } } } |
Figure 2: Pseudocode for k-Core Pull computation
Performance
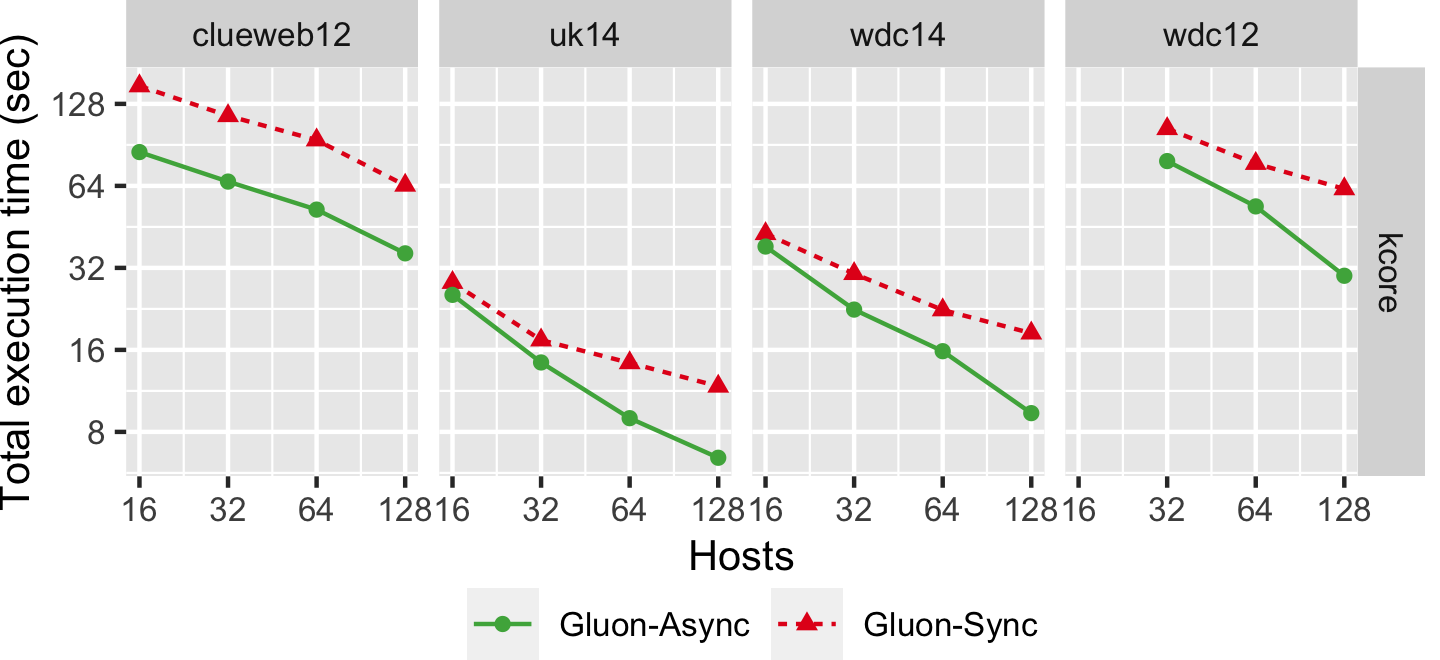
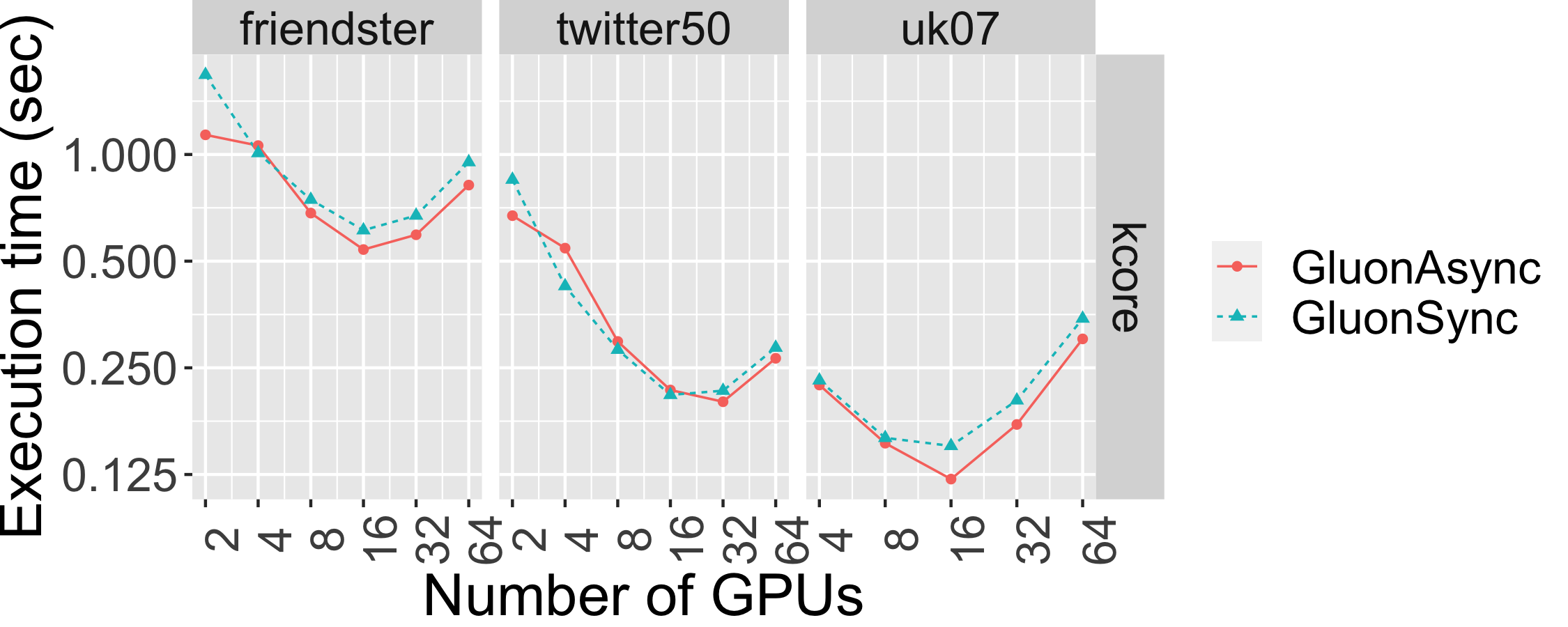
The graph below shows the strong scaling of kcore-push using both Bulk Synchronous Parallel (Gluon-Sync) and Bulk-Asynchronous Parallel (Gluon-Async) execution models which use a Gluon communication substrate. The experiments were conducted on Stampede Cluster (Stampede2), which is connected through Intel Omni-Path Architecture (peak bandwidth of 100Gbps). Each node has 2 Intel Xeon Platinum 8160 “Skylake” CPUs with 24 cores per CPU and 192GB DDR4 RAM. We use up to 128 CPU machines, each with 48 threads. We run on 4 graphs: clueweb12, uk14, wdc14, and wdc12. Most are real-world web-crawls: the web data commons hyperlink graph. wdc12, is the largest publicly available dataset. wdc14, clueweb12, and uk14 are all other large web-crawls.