Getting Started
Overview
This document describes how to use the Galois system. Galois exploits the amorphous data-parallelism in iterative algorithms that manipulate dynamic data structures such as graphs and trees. The user expresses the algorithm using sequential Java code, but specifies the loops that contain parallelism using Galois Iterators. The resulting code has well-defined sequential semantics while allowing efficient parallelization.
Typically, an iterative algorithm obtains work items from a worklist and terminates once the worklist is empty. The processing of a work item may generate new work items that have to be added to the worklist. We refer to the node in the graph data structure that corresponds to a work item as an active node. We define active edges similarly but will ignore them in this document as they are treated in the same way as active nodes. The processing of an active node may touch other nodes (and edges) of the graph. This set of touched nodes is called the neighborhood of the active node. Figure 1 shows a sample graph with active nodes and their neighborhoods.
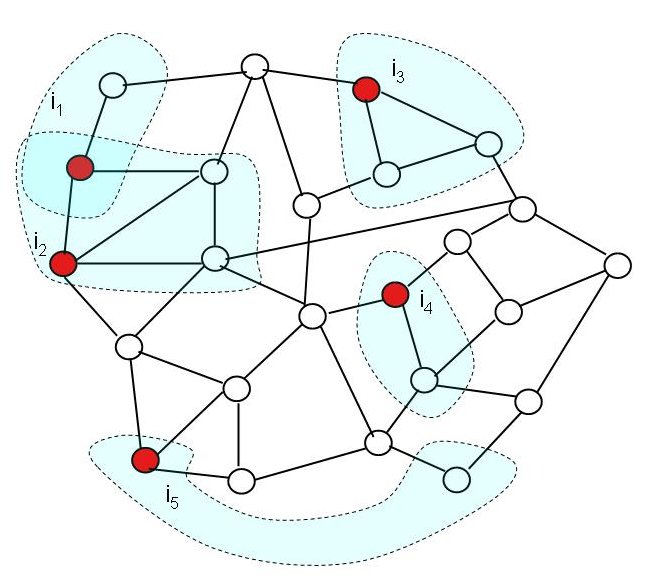
Figure 1: Graph with active nodes (red) and their neighborhoods (shaded blue regions).
In many algorithms, the order in which the active nodes are processed is irrelevant. In other algorithms, a partial or full order of processing active nodes must be followed. Aside from these ordering constraints (if any), it is easy to see from Figure 1 that active nodes can be processed in parallel as long as their neighborhoods do not overlap. In fact, even overlapping neighborhoods do not prevent parallel execution as long as the overlapped region is only read. Parallel execution is permissible in these cases because updates to the graph affect disjoint regions. Hence, the result of the parallel execution is identical to the result of a serial execution. We call this type of parallelism amorphous data-parallelism.
The current Galois release includes a dozen benchmarks representing important applications from a broad range of domains. These benchmarks are written using a standard programming language (C++ or Java) and use Galois extensions and classes, which are necessary for correct concurrent execution. This tool is work in progress and everything described herein is subject to change.
An Irregular Application: Spanning Tree Construction
We now illustrate the concepts on the example of building a spanning tree of a graph. Here, the worklist is initialized with a randomly selected node from the graph, which corresponds to the root of the spanning tree. The algorithm iteratively builds the spanning tree by growing a component C, which initially contains just the root node. At each point there is a set of edges connecting nodes inside C with the rest of the graph, thus defining a "cut". In each iteration the algorithm selects a node n from the worklist and for each cross-cutting edge of n, it adds the corresponding neighbor to C. Because at each point we can examine any cross-cutting edge to augment the spanning tree, there is no ordering constraint in the algorithm. A possible implementation of the algorithm is:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | typedef Galois::Graph::FirstGraph<Node,void,false> Graph; typedef Graph::GraphNode GNode; typedef std::pair<GNode,GNode> Edge; Graph graph = /* create unidirected graph with no edge data */ std::vector<Edge> result; /* create a container for edges of spanning tree */ GNode root = /* pick the root for the spanning tree */ std::vector<GNode> worklist; worklist.push_back(root); graph.getData(root).in_mst = true; while (!worklist.empty()) { GNode src = worklist.back(); worklist.pop_back(); // Expand tree for (Graph::neighbor_iterator ii = graph.neighbor_begin(src), ei = graph.neighbor_end(src); ii != ei; ++ii) { GNode dst = *ii; Node& data = graph.getData(dst); if (data.in_mst) continue; result.push(Edge(src, dst)); data.in_mst = true; worklist.push_back(dst); } } |
In line 5, the code instantiates the input graph graph and
populates it with nodes. In line 6 we create a bag that will hold the edges in
the spanning tree. In line 7, we select a node from the graph to be the root of
the spanning tree, and in lines 10 and 11, we add it to a workset of nodes that
need to be processed. Finally, in lines 12-25 we keep expanding the tree by
processing a node from the workset. The loop terminates when all nodes have
been added to the spanning tree.
Galoizing a Program
Galois concepts
There are three steps that must be taken to convert a sequential Java program into a Galois compatible parallel program.
- The loop(s) that should be run in parallel must be written using
foreachconstructs. - The
foreachmust use one of the provided worklist classes. - The data structure(s) that will be accessed in parallel must be expressed using Galois-provided classes.
Conceptually, after performing these steps the parallel program looks as follows:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | typedef Galois::Graph::FirstGraph<Node,void,false> Graph; typedef Graph::GraphNode GNode; typedef std::pair<GNode,GNode> Edge; Graph graph = /* create unidirected graph with no edge data */ Galois::InsertBag<Edge> result; /* create a container for edges of spanning tree */ GNode root = /* pick the root for the spanning tree */ std::vector<GNode> worklist; worklist.push_back(root); graph.getData(root).in_mst = true; foreach (GNode src : worklist) { // Expand tree... } |
The main changes are in lines 6, and 12-14. In line 6, we replace the
std::vector type with a Galois::InsertBag type
(provided by the Galois library), which allows efficient concurrent additions.
Note that in line 5, we already use the Galois library-provided implementation
of a graph, which is safe for parallel execution. In lines 12-14, the
sequential for loop over worklist is replaced by a
foreach loop. The code above presents the conceptual
structure of the program. In the following section we describe how these
concepts are implemented in the Galois system.
Foreach loops and worklists
The Galois foreach loop is implemented as a call to the
runtime library, which takes three components.
- An iterator over the initial contents of the worklist.
- A function object representing the loop body.
- A set of rules that dictate the type and implementation of the worklist.
The source code for the spanning tree application in Galois is provided below:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | struct Process { Galois::InsertBag<Edge>& result; Process(Galois::InsertBag<Edge>& _result) : result(_result) { } void operator()(GNode src, Galois::UserContext<GNode>& ctx) { // Expand tree... } }; typedef Galois::Graph::FirstGraph<Node,void,false> Graph; typedef Graph::GraphNode GNode; typedef std::pair<GNode,GNode> Edge; Graph graph = /* create unidirected graph with no edge data */ Galois::InsertBag<Edge> result; /* create a container for edges of spanning tree */ GNode root = /* pick the root for the spanning tree */ std::vector<GNode> worklist; worklist.push_back(root); graph.getData(root).in_mst = true; Galois::for_each(initial.begin(), initial.end(), Process(result)); |
This code implements an unordered foreach loop. In lines 1-8, we
create a function object that implements the body of the parallel loop. The
function Galois::for_each takes an optional template parameter that
describes the worklist scheduler. In this example, we omit this
parameter and use the default scheduler.
The function takes three function parameters, the
first two are iterators to the initial work of the loop. The third is a
function object implementing template<C> void
operator()(T,C&) where T is the type of elements in
the initial collection of work and C will be bound by the Galois
library to the type of the runtime context, used to add work to the worklist
and perform other runtime actions from within the loop. The code for expanding
the tree remains the same except calls to add work must
be changed to call the runtime context object rather than the collection
containing the initial work (not shown here).
For more information
on these concepts, the reader is referred to the Foreach Usage and Tuning Hints sections.
Galois data structures
Galois programs must be careful about objects that could be accessed by two
different iterations of a foreach loop. Such objects need special,
data-structure specific logic to describe the relationship between method calls
and how to undo modifications to their state. Currently, we provide a set of
classes that are safe to be shared between parallel iterations, including
graphs and other collection classes. These classes are located in the Galois
namespace and its subspaces. Any program that has shared objects that are not
instances of these classes will probably produce incorrect results when run
concurrently.
Galois provides several graph classes that share a common interface. For
the spanning tree example, the graph over which we build the spanning tree is
implemented using a general graph (Galois::Graph::FirstGraph).
A FirstGraph has several template parameters that indicate the
type of node and edge data and whether the graph is directed or undirected.
The graph of the spanning tree application does not require the existence of
data on the edges. To create a graph without edge data, we pass
void as the type of the edge data.
Controlling conflict detection
Each iteration of the for_each loop visits the neighbors of a
node, examines the value of their data, potentially modifies the data of some
neighboring nodes, and updates the collection of tree edges. By default, an
iteration calling a graph method acquires ownership of the nodes and edges the
method manipulates, and also saves undo information when needed. Note: the
current version of Galois, version 2.1, does not support saving undo
information. Version 2.0 does support saving undo information.
Therefore, in the code above, each iteration will try to acquire ownership of
src, all its neighbors, and their corresponding node data. In
addition, for each modification made to user data, the iteration must store
appropriate information in order to be able to undo the speculative
side-effects of actions it performs. Such actions usually have a performance
impact and reduce the amount of extracted parallelism.
The following simple observations help us optimize the above mentioned
overheads. First, by calling graph.neighbor_begin(GNode) an
iteration acquires ownership on each neighbor of src. Therefore,
subsequent calls that refer to those nodes, such as calling
graph.getData(GNode), can skip this task. Additionally, since each
node has its own private data item, protecting the node effectively protects
its associated data item too. Finally, when the iteration updates the
collection of result edges and the worklist, the iteration cannot fail anymore
and is no longer considered speculative. As a result, no undo information needs
to be stored here.
In order to convey this information to the runtime system, Galois object method calls may take an additional parameter, one of Galois::ALL, Galois::CHECK_CONFLICT, Galois::SAVE_UNDO, or Galois::NONE, that dictates what support the runtime will provide for each call. By default, the runtime assumes Galois::ALL. The optimized version of the method is provided below.
| 1 2 3 4 5 6 7 8 9 10 | // Expand tree for (Graph::neighbor_iterator ii = graph.neighbor_begin(src, Galois::CHECK_CONFLICT), ei = graph.neighbor_end(src, Galois::CHECK_CONFLICT); ii != ei; ++ii) { GNode dst = *ii; Node& data = graph.getData(dst, Galois::NONE); if (data.in_mst) continue; result.push(Edge(src, dst)); data.in_mst = true; ctx.push(dst); } |
In the current version of Galois, the InsertBag and the runtime context object do not support these flags, so care must be taken to ensure that calls to these objects happen after any possiblity of an iteration aborting. One such place is at the end of the iteration.
For a full list of available flags to control the Galois collection methods, please refer to the Tuning Hints section.
Compiling and Running a Galois Program
The Galois system uses cmake to
generate Makefiles; after these are generated, a simple make
command will build the Galois system and all distributed benchmarks.
To run a benchmark, just run the executable file in the appropriate
directory, which is under apps/appname.
A complete transcript of commands (and their outputs) to download, build and
run the spanning tree example application is the following. Lines beginning
with $ are commands to run; lines without $ are
the output of commands.
| $ $ $ $ $ $ $ | wget http://iss.ices.utexas.edu/projects/galois/downloads/Galois-2.1.8.tar.gz > /dev/null tar xzf Galois-2.1.8.tar.gz cd Galois-2.1.8/build mkdir default; cd default cmake ../.. > /dev/null make > /dev/null apps/spanningtree/spanningtree 0 ../../inputs/structured/torus5.gr INFO: ThreadPool Using maxwell for thread assignment policy INFO: CommandLine apps/spanningtree/spanningtree 0 /h1/ddn/w/Galois-2.1.8/inputs/structured/torus5.gr INFO: Hostname maxwell Lonestar Benchmark Suite v3.0 (C++) Copyright (C) 2011 The University of Texas at Austin http://iss.ices.utexas.edu/lonestar/ application: Spanning-tree Algorithm Compute the spanning tree (not mimimal) of a graph Edges in spanning tree: 31 STAT SINGLE NodeSize (null) 96 STAT SINGLE Conflicts (null) 0 STAT SINGLE Iterations (null) 32 STAT SINGLE Time (null) 1 STAT DISTRIBUTION 0 ConflictsDistribution (null) n: 1 ave: 0.0 min: 0 max: 0 stdev: 0.0 STAT DISTRIBUTION 0 IterationsDistribution (null) n: 1 ave: 32.0 min: 32 max: 32 stdev: 0.0 |
The output lines beginning with INFO or STAT
are produced by the runtime system to facilitate performance experiments
and data collection. For instance, the line STAT SINGLE Time (null) 1
indicates that the execution took 1 millisecond.
